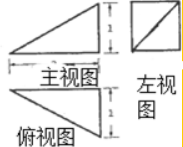
题目内容
6.已知$\frac{π}{2}$<θ<π,且sinθ=$\frac{{2\sqrt{2}}}{3}$,则tan$\frac{θ}{2}$=$\sqrt{2}$.分析 由题意结合三角函数公式易得tan$\frac{θ}{2}$的方程,结合角的范围,解方程可得.
解答 解:∵sinθ=$\frac{{2\sqrt{2}}}{3}$,∴2sin$\frac{θ}{2}$cos$\frac{θ}{2}$=$\frac{2\sqrt{2}}{3}$,
∴$\frac{2sin\frac{θ}{2}cos\frac{θ}{2}}{si{n}^{2}\frac{θ}{2}+co{s}^{2}\frac{θ}{2}}$=$\frac{2\sqrt{2}}{3}$,
∴$\frac{2tan\frac{θ}{2}}{ta{n}^{2}\frac{θ}{2}+1}$=$\frac{2\sqrt{2}}{3}$,
又∵$\frac{π}{2}$<θ<π,
∴$\frac{π}{4}$<$\frac{θ}{2}$<$\frac{π}{2}$,
∴tan$\frac{θ}{2}$>1,
解方程可得tan$\frac{θ}{2}$=$\sqrt{2}$
故答案为:$\sqrt{2}$
点评 本题考查三角函数化简求值,涉及二倍角公式,属基础题.

练习册系列答案
相关题目
17.下列函数既是偶函数又是周期为π的函数是( )
| A. | y=cos(x-$\frac{3π}{2}$) | B. | y=sin2x-cos2x | C. | y=cos2$\frac{x}{2}$ | D. | y=tan2x |
16.在面积为1的△ABC内部随机选取一点P,则△PBC面积大于$\frac{1}{4}$的概率为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{4}{9}$ | D. | $\frac{9}{16}$ |