题目内容
6.设函数f(x)=$\frac{2+lnx}{x}$.(1)求函数f(x)的单调区间和极值;
(2)如果对任意的x1,x2∈[1,+∞),有|{f(x1)-f(x2)|≥k|${\frac{1}{x_1}$-$\frac{1}{x_2}}$|成立,求实数k的最大值.
分析 (1)求函数的导数,利用导数的正负,可得函数f(x)的单调区间,从而可求实数a的值及f(x)的极值;
(2)根据不等式单调函数的单调性关系,将不等式进行转化,利用导数求函数的最值即可得到结论.
解答 解:(1)函数的f(x)的导数f′(x)=-$\frac{1+lnx}{{x}^{2}}$=0,
∴x=$\frac{1}{e}$,
∴f(x)在(0,$\frac{1}{e}$)上单调递增,在($\frac{1}{e}$,+∞)单调递减,
故f(x)在x=$\frac{1}{e}$处取得极大值e,无极小值;
(2)由(1)的结论知,f(x)在[1,+∞)上单调递减,不妨设x1≥x2≥1,
则|f(x1)-f(x2)|≥k|${\frac{1}{x_1}$-$\frac{1}{x_2}}$|,f(x2)-f(x1)≥k($\frac{1}{x_2}}$-${\frac{1}{x_1}$),
?f(x2)-k•$\frac{1}{x_2}}$≥f(x1)-k•${\frac{1}{x_1}$,
?函数F(x)=f(x)-$\frac{k}{x}$=$\frac{2-k+lnx}{x}$在[1,+∞)上单调递减,
则F′(x)=$\frac{k-1-lnx}{{x}^{2}}$≤0在[1,+∞)上恒成立,
∴k≤1+lnx在[1,+∞)上恒成立,
在[1,+∞)上,(1+lnx)min=1,
故k≤1,
∴实数k的最大值为1.
点评 本题主要考查导数的综合应用,考查函数的单调性,函数极值,最值,正确求出导数是解决本题的关键.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
14.已知t>0,若${∫}_{0}^{t}$(2x-2)dx=8,则t=( )
| A. | 1 | B. | -2 | C. | -2或4 | D. | 4 |
11.已知向量$\overrightarrow{a}$=(λ,1),向量$\overrightarrow{b}$=(2,1+λ),且$\overrightarrow{a}$与$\overrightarrow{a}$-$\overrightarrow{b}$垂直,则λ的值为( )
| A. | 0 | B. | 0或3 | C. | -3或0 | D. | 4 |
18.“φ=$\frac{π}{2}$,”是“曲线y=cos(2x+φ)”过原点的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
15.已知$\frac{a}{2+i}$=2-i(i为虚数单位),则实数a的值为( )
| A. | 5 | B. | -5 | C. | 0 | D. | 1 |
16.直角坐标系xoy中,以原点为极点,x轴的正半轴为极轴建立极坐标系,设点A,B分别在曲线C1:$\left\{{\begin{array}{l}{x=3+cosθ}\\{y=4+sinθ}\end{array}}$(θ为参数)和曲线C2:ρ=1上,则|AB|的最小值为( )
| A. | 3 | B. | $2\sqrt{5}$ | C. | $3\sqrt{5}$ | D. | $\sqrt{5}$ |
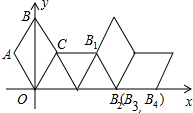 如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2014次,点B的落点依次为B1,B2,B3,…,则B2014的坐标为(1342,0).
如图在坐标系中放置一菱形OABC,已知∠ABC=60°,OA=1.先将菱形OABC沿x轴的正方向无滑动翻转,每次翻转60°,连续翻转2014次,点B的落点依次为B1,B2,B3,…,则B2014的坐标为(1342,0).