题目内容
11.已知向量$\overrightarrow{a}$=(λ,1),向量$\overrightarrow{b}$=(2,1+λ),且$\overrightarrow{a}$与$\overrightarrow{a}$-$\overrightarrow{b}$垂直,则λ的值为( )| A. | 0 | B. | 0或3 | C. | -3或0 | D. | 4 |
分析 求出$\overrightarrow{a}$-$\overrightarrow{b}$=(λ-2,-λ),由向量垂直可得其数量积为0,运用坐标表示,可得λ的方程,即可得到所求值.
解答 解:向量$\overrightarrow{a}$=(λ,1),向量$\overrightarrow{b}$=(2,1+λ),
即有$\overrightarrow{a}$-$\overrightarrow{b}$=(λ-2,-λ),
由$\overrightarrow{a}$与$\overrightarrow{a}$-$\overrightarrow{b}$垂直,
即有$\overrightarrow{a}$•($\overrightarrow{a}$-$\overrightarrow{b}$)=0,
即为λ(λ-2)-λ=0,
解得λ=0或3.
故选B.
点评 本题考查向量的垂直与向量的数量积的关系,属基础题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案 宝贝计划期末冲刺夺100分系列答案
宝贝计划期末冲刺夺100分系列答案
相关题目
9.用反证法证明命题“若a+b+c≥0,abc≤0,则a、b、c三个实数中最多有一个小于零”的反设内容为( )
| A. | a、b、c三个实数中最多有一个不大于零 | |
| B. | a、b、c三个实数中最多有两个小于零 | |
| C. | a、b、c三个实数中至少有两个小于零 | |
| D. | a、b、c三个实数中至少有一个不大于零 |
3.已知全集U={1,2,3,4,5,6,7,8},集合A={1,4,7},集合B={1,3,4,6,8},则(∁UA)∩B=( )
| A. | {1,4} | B. | {3,6,8} | C. | {1,2,4,5,7} | D. | {2,3,5,6,7,8} |
1.函数$y=sin(2x+\frac{5π}{2})$的最小正周期是( )
| A. | π | B. | 2π | C. | $\frac{π}{2}$ | D. | 4π |
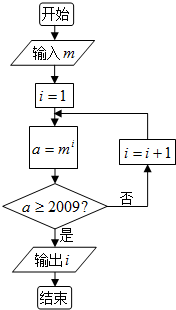 阅读框图,若输入m=3,则输出i=7.(参考数值:log32009≈6.923)
阅读框图,若输入m=3,则输出i=7.(参考数值:log32009≈6.923)