题目内容
15.已知$\frac{a}{2+i}$=2-i(i为虚数单位),则实数a的值为( )| A. | 5 | B. | -5 | C. | 0 | D. | 1 |
分析 由复数代数形式的除法运算化简$\frac{a}{2+i}$,然后由复数相等的条件得方程组,解方程组即可得到实数a的值.
解答 解:由$\frac{a}{2+i}$=$\frac{a(2-i)}{(2+i)(2-i)}=\frac{2a-ai}{5}=\frac{2a}{5}-\frac{a}{5}i$,
由复数相等的条件得:$\left\{\begin{array}{l}{\frac{2a}{5}=2}\\{-\frac{a}{5}=-1}\end{array}\right.$,
解得:a=5.
故选:A.
点评 本题考查了复数代数形式的乘除运算,考查了复数相等的条件,是基础题.

练习册系列答案
相关题目
13.在平行四边形ABCD中,点E是BC的中点,$\overrightarrow{BA}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,则$\overrightarrow{DE}$=( )
| A. | $\overrightarrow{a}-\frac{1}{2}\overrightarrow{b}$ | B. | $\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$ | C. | -$\overrightarrow{a}-\frac{1}{2}\overrightarrow{b}$ | D. | -$\overrightarrow{a}+\frac{1}{2}\overrightarrow{b}$ |
3.已知全集U={1,2,3,4,5,6,7,8},集合A={1,4,7},集合B={1,3,4,6,8},则(∁UA)∩B=( )
| A. | {1,4} | B. | {3,6,8} | C. | {1,2,4,5,7} | D. | {2,3,5,6,7,8} |
10.已知an=$\frac{n+10}{2n+1}$,Tn是数列{an}的前n项积,当Tn取到最大值时,n的值为( )
| A. | 9 | B. | 8 | C. | 8或9 | D. | 9或10 |
7.给定81个数排成如图所示的数表,若每行9个数与每列的9个数按表中顺序构成等差数列,且表中正中间一个数a55=5,则表中所有数之和为405.
| a11 | a12 | … | a19 |
| a21 | a22 | … | a29 |
| … | … | … | … |
| a91 | a92 | … | a99 |
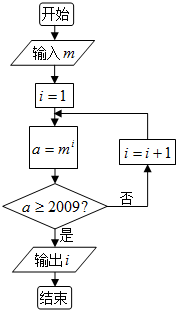 阅读框图,若输入m=3,则输出i=7.(参考数值:log32009≈6.923)
阅读框图,若输入m=3,则输出i=7.(参考数值:log32009≈6.923)