题目内容
4．
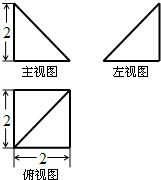如图为一个几何体的三视图，其主、左视图均为等腰直角三角形，俯视图的外轮廓是正方形（尺寸如图），则该几何体的外接球的表面积为（ ）| A． | 4π | B． | 8π | C． | 12π | D． | 16π |
分析 由已知的三视图，可得该几何体是一个以俯视图为底面的四棱锥，求出该几何体的外接球的半径，可得答案．
解答 解：由已知的三视图，可得该几何体是一个以俯视图为底面的四棱锥，棱锥的底面是边长为2的正方形，棱锥的高为2，
故该几何体的外接球的直径为$\sqrt{3}$，半径为$\sqrt{3}$，
∴该几何体的外接球的表面积为4π×3=12π，
故选：C．
点评 本题考查求该几何体的外接球的表面积，其中根据已知分析出几何体的形状，是解答的关键．
练习册系列答案
相关题目
12．已知点M（-1，2），N（3，3），若直线l：kx-y-2k-1=0与线段MN相交，则k的取值范围是（ ）
| A． | [4，+∞） | B． | （-∞，-1] | C． | （-∞，-1]∪[4，+∞） | D． | [-1，4] |
16．在△ABC中，B=$\frac{π}{6}$，c=150，b=50$\sqrt{3}$，则△ABC为（ ）
| A． | 直角三角形 | B． | 等腰三角形或直角三角形 | ||
| C． | 等边三角形 | D． | 等腰三角形 |
14．班主任为了对本班学生的考试成绩进行分析，决定从全班25名女同学，15名男同学中随机抽取一个容量为8的样本进行分析．随机抽出8位，他们的数学分数从小到大排序是：60、65、70、75、80、85、90、95，物理分数从小到大排序是：72、77、80、84、88、90、93、95．
（Ⅰ）如果按性别比例分层抽样，男女同学分别抽取多少人？
（Ⅱ）若这8位同学的数学、物理分数对应如下表：
根据上表数据用变量y与x的相关系数或散点图说明物理成绩y与数学成绩x之间是否具有线性相关性？如果具有线性相关性，求y与x的线性回归方程（系数精确到0.01）；如果不具有线性相关性，请说明理由．
参考公式：相关系数$r=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sqrt{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}\sqrt{\sum_i^n{（{y_i}-\overline y}}{）^2}}}$；回归直线的方程是：$\widehat{y}$=bx+a．
其中对应的回归估计值b=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，a=$\overline{y}$-b$\overline{x}$；
参考数据：$\overline{x}$=77.5，$\overline{y}$=85，$\sum_{i=1}^{8}$（x1-$\overline{x}$）2≈1050，$\sum_{i=1}^{8}$（y1-$\overline{y}$）2≈456；$\sum_{i=1}^{8}$（x1-$\overline{x}$）（y1-$\overline{y}$）≈688，$\sqrt{1050}$≈32.4，$\sqrt{456}$≈21.4，$\sqrt{550}$≈23.5．
（Ⅰ）如果按性别比例分层抽样，男女同学分别抽取多少人？
（Ⅱ）若这8位同学的数学、物理分数对应如下表：
| 学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 数学分数x | 60 | 65 | 70 | 75 | 80 | 85 | 90 | 95 |
| 物理分数y | 72 | 77 | 80 | 84 | 88 | 90 | 93 | 95 |
参考公式：相关系数$r=\frac{{\sum_{i=1}^n{（{x_i}-\overline x）（{y_i}-\overline y）}}}{{\sqrt{\sum_{i=1}^n{{{（{x_i}-\overline x）}^2}}}\sqrt{\sum_i^n{（{y_i}-\overline y}}{）^2}}}$；回归直线的方程是：$\widehat{y}$=bx+a．
其中对应的回归估计值b=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，a=$\overline{y}$-b$\overline{x}$；
参考数据：$\overline{x}$=77.5，$\overline{y}$=85，$\sum_{i=1}^{8}$（x1-$\overline{x}$）2≈1050，$\sum_{i=1}^{8}$（y1-$\overline{y}$）2≈456；$\sum_{i=1}^{8}$（x1-$\overline{x}$）（y1-$\overline{y}$）≈688，$\sqrt{1050}$≈32.4，$\sqrt{456}$≈21.4，$\sqrt{550}$≈23.5．