题目内容
19.使方程√8x−x2-x-m=0有两个不等的实数解,则实数m的取值范围是0≤m<4√2-4.分析 由√8x−x2-x-m=0得√8x−x2=x+m,设y=√8x−x2和y=x+m,利用数形结合进行求解即可.
解答 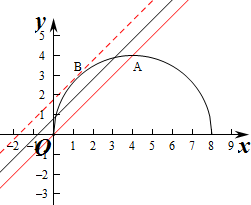 解:由√8x−x2-x-m=0得√8x−x2=x+m,设y=√8x−x2和y=x+m,
解:由√8x−x2-x-m=0得√8x−x2=x+m,设y=√8x−x2和y=x+m,
则8x-x2=y2,
即(x-4)2+y2=16,(y≥0),
作出对应的图象如图:
当直线y=x+m经过点O时,m=0,此时直线和半圆有两个交点,
当直线y=x+m与半圆相切时,(m>0),
圆心(4,0)到直线的距离d=|4+m|√2=4,
即|m+4|=4√2,
解得m=4√2-4,或m=-4√2-4,(舍),
故方程√8x−x2-x-m=0有两个不等的实数解,
则0≤m<4√2-4,
故答案为:0≤m<4√2-4
点评 本题主要考查函数和方程的应用,利用条件转化为两个函数之间的关系,利用数形结合是解决本题的关键.

练习册系列答案
相关题目
14.已知圆C1:(x+2)2+(y-3)2=5与圆C2相交于A(0,2),B(-1,1)两点,且四边形C1AC2B为平行四形,则圆C2的方程为( )
| A. | (x-1)2+y2=5 | B. | (x-1)2+y2=\frac{9}{2} | C. | (x-\frac{1}{2})2+(y-\frac{1}{2})2=5 | D. | (x-\frac{1}{2})2+(y-\frac{1}{2})2=\frac{9}{2} |
4.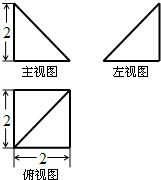 如图为一个几何体的三视图,其主、左视图均为等腰直角三角形,俯视图的外轮廓是正方形(尺寸如图),则该几何体的外接球的表面积为( )
如图为一个几何体的三视图,其主、左视图均为等腰直角三角形,俯视图的外轮廓是正方形(尺寸如图),则该几何体的外接球的表面积为( )
 如图为一个几何体的三视图,其主、左视图均为等腰直角三角形,俯视图的外轮廓是正方形(尺寸如图),则该几何体的外接球的表面积为( )
如图为一个几何体的三视图,其主、左视图均为等腰直角三角形,俯视图的外轮廓是正方形(尺寸如图),则该几何体的外接球的表面积为( )| A. | 4π | B. | 8π | C. | 12π | D. | 16π |
8.已知sin(3π+α)=\frac{1}{3},则cos2α等于( )
| A. | \frac{7}{9} | B. | -\frac{7}{9} | C. | \frac{8}{9} | D. | -\frac{8}{9} |