题目内容
16.在△ABC中,B=$\frac{π}{6}$,c=150,b=50$\sqrt{3}$,则△ABC为( )| A. | 直角三角形 | B. | 等腰三角形或直角三角形 | ||
| C. | 等边三角形 | D. | 等腰三角形 |
分析 由已知及正弦定理可求得sinC=$\frac{csinB}{b}$=$\frac{\sqrt{3}}{2}$,利用大边对大角可得$\frac{π}{6}$<C<π,可解得:C,A的值,从而得解.
解答 解:由已知及正弦定理可得:sinC=$\frac{csinB}{b}$=$\frac{150×sin\frac{π}{6}}{50\sqrt{3}}$=$\frac{\sqrt{3}}{2}$.
∵c=150>b=50$\sqrt{3}$,
∴$\frac{π}{6}$<C<π,可解得:C=$\frac{π}{3}$或$\frac{2π}{3}$.
∴解得:A=$\frac{π}{2}$或$\frac{π}{6}$.
故选:B.
点评 本题主要考查了正弦定理,大边对大角等知识的应用,属于基本知识的考查.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.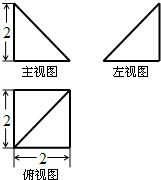 如图为一个几何体的三视图,其主、左视图均为等腰直角三角形,俯视图的外轮廓是正方形(尺寸如图),则该几何体的外接球的表面积为( )
如图为一个几何体的三视图,其主、左视图均为等腰直角三角形,俯视图的外轮廓是正方形(尺寸如图),则该几何体的外接球的表面积为( )
 如图为一个几何体的三视图,其主、左视图均为等腰直角三角形,俯视图的外轮廓是正方形(尺寸如图),则该几何体的外接球的表面积为( )
如图为一个几何体的三视图,其主、左视图均为等腰直角三角形,俯视图的外轮廓是正方形(尺寸如图),则该几何体的外接球的表面积为( )| A. | 4π | B. | 8π | C. | 12π | D. | 16π |
1.(1)某企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系,随机抽取了72名员工进行调查,所得的数据如表所示:
对于人力资源部的研究项目,根据上述数据你能得出什么结论?
(友情提示:当Χ2>3.841时,有95%的把握说事件A与B有关;当Χ2>6.635时,有99%的把握说事件A与B有关; 当Χ2<3.841时认为事件A与B无关.)
(2)高中数学必修3第三章内容是概率.概率包括事件与概率,古典概型,概率的应用.事件与概率又包括随机现象,事件与基本事件空间,频率与概率,概率的加法公式.请画出它们之间的知识结构图.
| 积极支持改革 | 不太支持改革 | 合 计 | |
| 工作积极 | 28 | 8 | 36 |
| 工作一般 | 16 | 20 | 36 |
| 合 计 | 44 | 28 | 72 |
(友情提示:当Χ2>3.841时,有95%的把握说事件A与B有关;当Χ2>6.635时,有99%的把握说事件A与B有关; 当Χ2<3.841时认为事件A与B无关.)
(2)高中数学必修3第三章内容是概率.概率包括事件与概率,古典概型,概率的应用.事件与概率又包括随机现象,事件与基本事件空间,频率与概率,概率的加法公式.请画出它们之间的知识结构图.
8.已知sin(3π+α)=$\frac{1}{3}$,则cos2α等于( )
| A. | $\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{8}{9}$ | D. | -$\frac{8}{9}$ |
6.已知an=($\frac{1}{2}$)n,把数列{an}的各项排列成如下的三角形状,

记A(m,n)表示第m行的第n个数,则A(10,13)=( )

记A(m,n)表示第m行的第n个数,则A(10,13)=( )
| A. | ${(\frac{1}{2})^{93}}$ | B. | ${(\frac{1}{2})^{92}}$ | C. | ${(\frac{1}{2})^{94}}$ | D. | ${(\frac{1}{2})^{112}}$ |
 如图,棱锥的底ABCD是一个矩形,AC与BD交于M,VM是棱锥的高,若VM=4cm,AB=4cm,VC=5cm,求棱锥的体积.
如图,棱锥的底ABCD是一个矩形,AC与BD交于M,VM是棱锥的高,若VM=4cm,AB=4cm,VC=5cm,求棱锥的体积.