题目内容
13.已知双曲线C是以原点为中心,其右焦点为F(3,0),离心率为$\frac{3}{2}$,则双曲线C的方程是$\frac{x^2}{4}-\frac{y^2}{5}=1$,渐近线方程是$y=±\frac{{\sqrt{5}}}{2}x$.分析 根据题意,双曲线的焦点在x轴上,c=3,$\frac{c}{a}$=$\frac{3}{2}$,即可得出双曲线的标准方程和渐近线方程.
解答 解:由题意,双曲线的焦点在x轴上,c=3,$\frac{c}{a}$=$\frac{3}{2}$,
∴a=2,b=$\sqrt{5}$,
∴双曲线C的标准方程$\frac{x^2}{4}-\frac{y^2}{5}=1$;其渐近线方程为$y=±\frac{{\sqrt{5}}}{2}x$.
故答案为:$\frac{x^2}{4}-\frac{y^2}{5}=1$;$y=±\frac{{\sqrt{5}}}{2}x$
点评 本题给出双曲线满足的条件,求双曲线的标准方程和渐近线.着重考查了双曲线的标准方程与简单几何性质等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.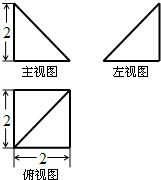 如图为一个几何体的三视图,其主、左视图均为等腰直角三角形,俯视图的外轮廓是正方形(尺寸如图),则该几何体的外接球的表面积为( )
如图为一个几何体的三视图,其主、左视图均为等腰直角三角形,俯视图的外轮廓是正方形(尺寸如图),则该几何体的外接球的表面积为( )
 如图为一个几何体的三视图,其主、左视图均为等腰直角三角形,俯视图的外轮廓是正方形(尺寸如图),则该几何体的外接球的表面积为( )
如图为一个几何体的三视图,其主、左视图均为等腰直角三角形,俯视图的外轮廓是正方形(尺寸如图),则该几何体的外接球的表面积为( )| A. | 4π | B. | 8π | C. | 12π | D. | 16π |
1.(1)某企业人力资源部为了研究企业员工工作积极性和对待企业改革态度的关系,随机抽取了72名员工进行调查,所得的数据如表所示:
对于人力资源部的研究项目,根据上述数据你能得出什么结论?
(友情提示:当Χ2>3.841时,有95%的把握说事件A与B有关;当Χ2>6.635时,有99%的把握说事件A与B有关; 当Χ2<3.841时认为事件A与B无关.)
(2)高中数学必修3第三章内容是概率.概率包括事件与概率,古典概型,概率的应用.事件与概率又包括随机现象,事件与基本事件空间,频率与概率,概率的加法公式.请画出它们之间的知识结构图.
| 积极支持改革 | 不太支持改革 | 合 计 | |
| 工作积极 | 28 | 8 | 36 |
| 工作一般 | 16 | 20 | 36 |
| 合 计 | 44 | 28 | 72 |
(友情提示:当Χ2>3.841时,有95%的把握说事件A与B有关;当Χ2>6.635时,有99%的把握说事件A与B有关; 当Χ2<3.841时认为事件A与B无关.)
(2)高中数学必修3第三章内容是概率.概率包括事件与概率,古典概型,概率的应用.事件与概率又包括随机现象,事件与基本事件空间,频率与概率,概率的加法公式.请画出它们之间的知识结构图.
8.已知sin(3π+α)=$\frac{1}{3}$,则cos2α等于( )
| A. | $\frac{7}{9}$ | B. | -$\frac{7}{9}$ | C. | $\frac{8}{9}$ | D. | -$\frac{8}{9}$ |
2.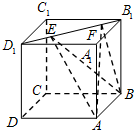 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{1}{2}$,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{1}{2}$,则下列结论中错误的是( )
 如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{1}{2}$,则下列结论中错误的是( )
如图,正方体ABCD-A1B1C1D1的棱长为1,线段B1D1上有两个动点E、F,且EF=$\frac{1}{2}$,则下列结论中错误的是( )| A. | AC⊥BE | B. | △AEF的面积与△BEF的面积相等 | ||
| C. | EF∥平面ABCD | D. | 三棱锥A-BEF的体积为定值 |
3.应试教育下的高三学生身体素质堪忧,教育部门对某市100名高三学生的课外体育锻炼时间进行调查.他们的课外体育锻炼时间及相应的频数如下表:
将学生日均课外体育运动时间在$[\frac{2}{3},1)$上的学生评价为“课外体育达标”.
(1)根据已知条件完成下面的2×2列联表:
(2)根据列联表的数据,若按95%的可靠性要求,能否认为“课外体育达标”与性别有关?
附:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 运动时间 (单位:小时) | $[0,\frac{1}{6})$ | $[\frac{1}{6},\frac{1}{3})$ | $[\frac{1}{3},\frac{1}{2})$ | $[\frac{1}{2},\frac{2}{3})$ | $[\frac{2}{3},\frac{5}{6})$ | $[\frac{5}{6},1)$ |
| 总人数 | 10 | 18 | 22 | 25 | 20 | 5 |
(1)根据已知条件完成下面的2×2列联表:
| 课外体育不达标 | 课外体育达标 | 合计 | |
| 男 | |||
| 女 | 10 | 55 | |
| 合计 |
附:${Χ^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d.
| 参考数据 | 当Χ2≤2.706时,无充分证据判定变量A,B有关联,可以认为两变量无关联; |
| 当Χ2>2.706时,有90%的把握判定变量A,B有关联; | |
| 当Χ2>3.841时,有95%的把握判定变量A,B有关联; | |
| 当Χ2>6.635时,有99%的把握判定变量A,B有关联. |