题目内容
5.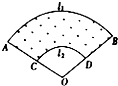 某小区设计的花坛形状如图中的阴影部分,已知$\widehat{AB}$和$\widehat{CD}$所在圆的圆心都是点O,$\widehat{AB}$的长为l1,$\widehat{CD}$的长为l2,AC=BD=d,则花坛的面积为$\frac{1}{2}$d(l1+l2).
某小区设计的花坛形状如图中的阴影部分,已知$\widehat{AB}$和$\widehat{CD}$所在圆的圆心都是点O,$\widehat{AB}$的长为l1,$\widehat{CD}$的长为l2,AC=BD=d,则花坛的面积为$\frac{1}{2}$d(l1+l2).
分析 根据扇形面积公式,弧长公式及几何体的面积之间的关系即可求解.
解答 解:设大扇形半径为R,小扇形半径为r,圆心角的度数为n,则由l=$\frac{nπR}{180}$可得:R=$\frac{180{l}_{1}}{nπ}$,r=$\frac{180{l}_{2}}{nπ}$,
则花坛的面积为:$\frac{1}{2}×{l}_{1}×R$-$\frac{1}{2}×{l}_{2}×r$
=$\frac{1}{2}$×l1×$\frac{180{l}_{1}}{nπ}$-$\frac{1}{2}×{l}_{2}×$$\frac{180{l}_{2}}{nπ}$
=$\frac{90}{nπ}({{l}_{1}}^{2}-{{l}_{2}}^{2})$
=$\frac{1}{2}×\frac{180}{nπ}$($\frac{nπR}{180}-\frac{nπr}{180}$)×(l1+l2)
=$\frac{1}{2}$(l1+l2)(R-r)
=$\frac{1}{2}$d(l1+l2).
故答案为:$\frac{1}{2}$d(l1+l2).
点评 本题主要考查了扇形面积公式的应用,属于基本知识的考查.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
15.已知不等式|x+a|+|x-3|≤|x-4|的解集包含[2,3],则a的取值范围为( )
| A. | [-3,-2] | B. | [-2,0] | C. | [-3,0] | D. | [-2,1] |
13.函数f(x)(x∈R)满足f(1)=1,f′(1)=1,f′(x)<$\frac{1}{2}$,f(x2)<$\frac{1}{2}$x2+$\frac{1}{2}$.
| A. | (-∞.-1) | B. | (1,+∞) | C. | (-∞,-1)∪(1,+∞) | D. | (-1,1) |
17.函数y=3cos($\frac{2}{5}$x-$\frac{π}{6}$)的最小正周期是( )
| A. | $\frac{2\;π}{5}$ | B. | $\frac{5\;π}{2}$ | C. | 2π | D. | 5π |