题目内容
10.已知$sinx=\frac{1}{2}$且$x∈({\frac{π}{2},π})$,则sin2x=$-\frac{{\sqrt{3}}}{2}$.分析 由已知利用同角三角函数关系式可求cosx,利用二倍角的正弦函数公式即可求值.
解答 解:∵$sinx=\frac{1}{2}$且$x∈({\frac{π}{2},π})$,
∴cosx=-$\sqrt{1-si{n}^{2}x}$=-$\sqrt{1-(\frac{1}{2})^{2}}$=-$\frac{\sqrt{3}}{2}$.
∴sin2x=2sinxcosx=2×$\frac{1}{2}×(-\frac{\sqrt{3}}{2})$=$-\frac{{\sqrt{3}}}{2}$.
故答案为:$-\frac{{\sqrt{3}}}{2}$.
点评 本题主要考查了同角三角函数关系式,二倍角的正弦函数公式的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.已知x>2,则x+$\frac{4}{x-2}$的最小值为( )
| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
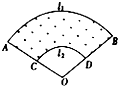 某小区设计的花坛形状如图中的阴影部分,已知$\widehat{AB}$和$\widehat{CD}$所在圆的圆心都是点O,$\widehat{AB}$的长为l1,$\widehat{CD}$的长为l2,AC=BD=d,则花坛的面积为$\frac{1}{2}$d(l1+l2).
某小区设计的花坛形状如图中的阴影部分,已知$\widehat{AB}$和$\widehat{CD}$所在圆的圆心都是点O,$\widehat{AB}$的长为l1,$\widehat{CD}$的长为l2,AC=BD=d,则花坛的面积为$\frac{1}{2}$d(l1+l2).