题目内容
20．设f（x）=x2+ax+3，不等式f（x）≥a对x∈R恒成立，则实数a的取值范围为-6≤a≤2．分析 问题转化为x2+ax+3-a≥0对x∈R恒成立，设g（x）=x2+ax+3-a，根据二次函数的性质得到不等式，解出即可．
解答 解：不等式f（x）≥a对x∈R恒成立，
等价于x2+ax+3-a≥0对x∈R恒成立，
设g（x）=x2+ax+3-a，
则只需△=a2-4（3-a）≤0即可，
解得：-6≤a≤2，
故答案为：-6≤a≤2．
点评 本题考查了二次函数的性质问题，考查转化思想，是一道基础题．
练习册系列答案
名校课堂系列答案
相关题目
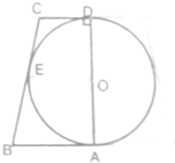如图，半圆O的直径为直角梯形垂直于底的腰，且切AB、BC、CD于A、E、D点，将其绕AD所在直线旋转一周，得到一个球与一个圆台，若球的表面积与圆台侧面积的比为3：4，求球的体积与圆台体积之比．
8．已知tanα=2，则$\frac{1+2sinαcosα}{{{{sin}^2}α-{{cos}^2}α}}$的值是（ ）
| A． | $\frac{1}{3}$ | B． | 3 | C． | -$\frac{1}{3}$ | D． | -3 |
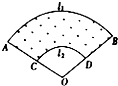某小区设计的花坛形状如图中的阴影部分，已知$\widehat{AB}$和$\widehat{CD}$所在圆的圆心都是点O，$\widehat{AB}$的长为l1，$\widehat{CD}$的长为l2，AC=BD=d，则花坛的面积为$\frac{1}{2}$d（l1+l2）．