题目内容
15.函数f(x)=$\frac{\sqrt{3x-{x}^{2}}}{x-1}$+log0.5(x-1)的定义域用区间表示为(1,3].分析 根据函数成立的条件即可求出函数的定义域.
解答 解:要使函数有意义,则$\left\{\begin{array}{l}{3x-x^2≥0}\\{x-1≠0}\\{x-1>0}\end{array}\right.$,
即$\left\{\begin{array}{l}{0≤x≤3}\\{x≠1}\\{x>1}\end{array}\right.$,
即1<x≤3,
即函数的定义域为(1,3],
故答案为:(1,3].
点评 本题主要考查函数的定义域的求解,要求熟练掌握常见函数成立的条件.

练习册系列答案
相关题目
3.在一次考试中,5名同学数学、物理成绩如表所示:
(Ⅰ)根据表中数据,求物理分y对数学分x的回归方程.
(Ⅱ)要从4名数学成绩在90分以上的同学中选出2名参加一项活动,以X表示选中的同学中物理成绩高于90分的人数,求随机变量X的分布列及期望.(附:回归方程$\widehat{y}$=bx+a中,b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$)
| 学生 | A | B | C | D | E |
| 数学(x分) | 89 | 91 | 93 | 95 | 97 |
| 物理(y分) | 87 | 89 | 89 | 92 | 93 |
(Ⅱ)要从4名数学成绩在90分以上的同学中选出2名参加一项活动,以X表示选中的同学中物理成绩高于90分的人数,求随机变量X的分布列及期望.(附:回归方程$\widehat{y}$=bx+a中,b=$\frac{\sum_{i=1}^{n}({x}_{i}-\overline{x})({y}_{i}-\overline{y})}{\sum_{i=1}^{n}({x}_{i}-\overline{x})^{2}}$,a=$\overline{y}$-b$\overline{x}$)
20.已知x>2,则x+$\frac{4}{x-2}$的最小值为( )
| A. | 6 | B. | 4 | C. | 3 | D. | 2 |
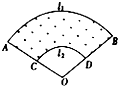 某小区设计的花坛形状如图中的阴影部分,已知$\widehat{AB}$和$\widehat{CD}$所在圆的圆心都是点O,$\widehat{AB}$的长为l1,$\widehat{CD}$的长为l2,AC=BD=d,则花坛的面积为$\frac{1}{2}$d(l1+l2).
某小区设计的花坛形状如图中的阴影部分,已知$\widehat{AB}$和$\widehat{CD}$所在圆的圆心都是点O,$\widehat{AB}$的长为l1,$\widehat{CD}$的长为l2,AC=BD=d,则花坛的面积为$\frac{1}{2}$d(l1+l2).