题目内容
14．已知全集U=R，集合A={x|x2-4x-5≤0}，B={x|x＜4}，C={x|x≥a}．（Ⅰ）求A∩（∁UB）； （Ⅱ）若A⊆C，求a的取值范围．
分析 （Ⅰ）求出A中不等式的解集确定出A，由全集U=R，及B求出B的补集，求出A与B补集的交集即可；
（Ⅱ）根据A，C，以及A为C的子集，确定出a的范围即可．
解答 解：（Ⅰ）∵全集U=R，B={x|x＜4}，
∴∁UB={x|x≥4}，
又∵A={x|x2-4x-5≤0}={x|-1≤x≤5}，
∴A∩（∁UB）={x|4≤x≤5}；
（Ⅱ）∵A={x|-1≤x≤5}，C={x|x≥a}，且A⊆C，
∴a的范围为a≤-1．
点评 此题考查了交、并、补集的混合运算，以及集合的包含关系判断及应用，熟练掌握各自的定义是解本题的关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
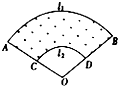某小区设计的花坛形状如图中的阴影部分，已知$\widehat{AB}$和$\widehat{CD}$所在圆的圆心都是点O，$\widehat{AB}$的长为l1，$\widehat{CD}$的长为l2，AC=BD=d，则花坛的面积为$\frac{1}{2}$d（l1+l2）．
3．在一次考试中，5名同学数学、物理成绩如表所示：
（Ⅰ）根据表中数据，求物理分y对数学分x的回归方程．
（Ⅱ）要从4名数学成绩在90分以上的同学中选出2名参加一项活动，以X表示选中的同学中物理成绩高于90分的人数，求随机变量X的分布列及期望．（附：回归方程$\widehat{y}$=bx+a中，b=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，a=$\overline{y}$-b$\overline{x}$）
| 学生 | A | B | C | D | E |
| 数学（x分） | 89 | 91 | 93 | 95 | 97 |
| 物理（y分） | 87 | 89 | 89 | 92 | 93 |
（Ⅱ）要从4名数学成绩在90分以上的同学中选出2名参加一项活动，以X表示选中的同学中物理成绩高于90分的人数，求随机变量X的分布列及期望．（附：回归方程$\widehat{y}$=bx+a中，b=$\frac{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）（{y}_{i}-\overline{y}）}{\sum_{i=1}^{n}（{x}_{i}-\overline{x}）^{2}}$，a=$\overline{y}$-b$\overline{x}$）