题目内容
已知椭圆C: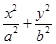 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为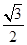 ,且在x轴上的顶点分别为
,且在x轴上的顶点分别为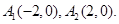
(1)求椭圆方程;
(2)若直线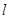 :
: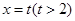 与
与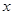 轴交于点T,P为
轴交于点T,P为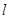 上异于T的任一点,直线
上异于T的任一点,直线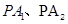 分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
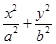 =1(a>b>0)的离心率为
=1(a>b>0)的离心率为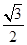 ,且在x轴上的顶点分别为
,且在x轴上的顶点分别为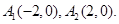
(1)求椭圆方程;
(2)若直线
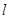 :
: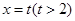 与
与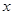 轴交于点T,P为
轴交于点T,P为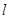 上异于T的任一点,直线
上异于T的任一点,直线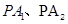 分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.
分别与椭圆交于M、N两点,试问直线MN是否通过椭圆的焦点?并证明你的结论.(1)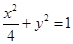 (2)见解析
(2)见解析
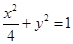 (2)见解析
(2)见解析(1)由e和a的值,可求出a,c进而求出b,所以椭圆的标准方程确定.
(2)设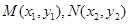 ,直线
,直线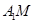 的方程为
的方程为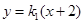 ,与椭圆方程联立解方程组可得
,与椭圆方程联立解方程组可得
M的坐标,同理由直线 的方程
的方程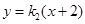 可求出N的坐标.可求出MN的方程,再令y=0,得直线MN与x轴的交点坐标它与右焦点坐标为
可求出N的坐标.可求出MN的方程,再令y=0,得直线MN与x轴的交点坐标它与右焦点坐标为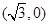 重合,可求出t值,若满足t>2,则存在,否则不存在
重合,可求出t值,若满足t>2,则存在,否则不存在
(1)由已知椭圆C的离心率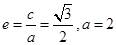 ,可得
,可得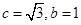
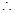 椭圆的方程为
椭圆的方程为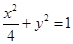
(2)设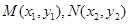 ,直线
,直线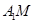 斜率为
斜率为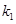
则直线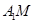 的方程为
的方程为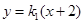
由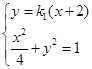 ,解得
,解得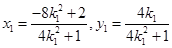
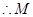 点坐标为
点坐标为 (
(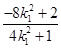 ,
,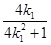 )
)
同理,设直线 的斜率为
的斜率为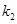 则
则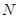 点坐标为(
点坐标为(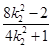 ,
,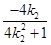 )
)
由直线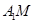 与直线
与直线 的交点
的交点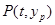 在直线
在直线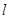 上
上
又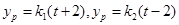 ,
,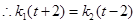 ,
,
又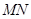 的方程为
的方程为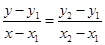 令
令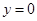 ,得
,得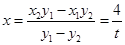
即直线MN与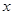 轴交点为
轴交点为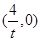 又
又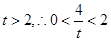
又椭圆右焦点为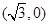 ,故当
,故当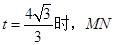 过椭圆的焦点
过椭圆的焦点
(2)设
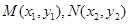 ,直线
,直线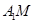 的方程为
的方程为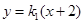 ,与椭圆方程联立解方程组可得
,与椭圆方程联立解方程组可得M的坐标,同理由直线
 的方程
的方程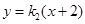 可求出N的坐标.可求出MN的方程,再令y=0,得直线MN与x轴的交点坐标它与右焦点坐标为
可求出N的坐标.可求出MN的方程,再令y=0,得直线MN与x轴的交点坐标它与右焦点坐标为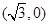 重合,可求出t值,若满足t>2,则存在,否则不存在
重合,可求出t值,若满足t>2,则存在,否则不存在(1)由已知椭圆C的离心率
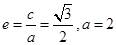 ,可得
,可得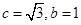
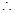 椭圆的方程为
椭圆的方程为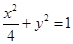
(2)设
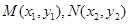 ,直线
,直线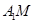 斜率为
斜率为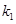
则直线
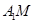 的方程为
的方程为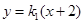
由
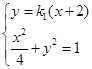 ,解得
,解得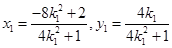
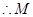 点坐标为
点坐标为 (
(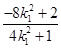 ,
,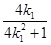 )
)同理,设直线
 的斜率为
的斜率为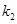 则
则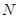 点坐标为(
点坐标为(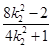 ,
,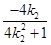 )
)由直线
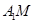 与直线
与直线 的交点
的交点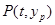 在直线
在直线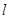 上
上又
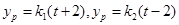 ,
,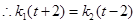 ,
,
又
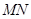 的方程为
的方程为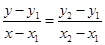 令
令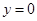 ,得
,得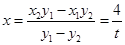
即直线MN与
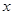 轴交点为
轴交点为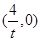 又
又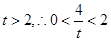
又椭圆右焦点为
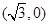 ,故当
,故当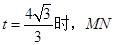 过椭圆的焦点
过椭圆的焦点
练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
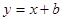 与曲线
与曲线 恰有一个公共点,
恰有一个公共点, 的取值范围是 。
的取值范围是 。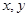 满足
满足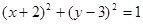 ,则
,则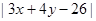 的最小值为
的最小值为 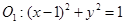 外切,与圆
外切,与圆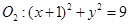 内切.
内切.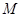 的轨迹
的轨迹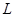 的方程;
的方程; 的直线
的直线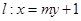 与轨迹
与轨迹 、
、 两点,请问
两点,请问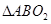 (
(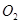 为圆
为圆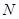 的面积是否存在最大值?若存在,求出这个最大值及直线
的面积是否存在最大值?若存在,求出这个最大值及直线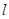 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由. =2
=2 ,则
,则 ·
· =________.
=________.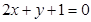 和
和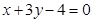 的交点且与直线
的交点且与直线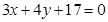 相切,求圆C的方程.
相切,求圆C的方程.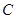 :
: 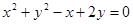 关于直线
关于直线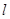 :
: 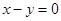 对称的圆的方程为_________.
对称的圆的方程为_________.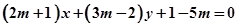 被圆
被圆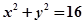 截得弦长的最小值为 .
截得弦长的最小值为 .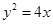 的焦点为圆心,且被
的焦点为圆心,且被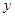 轴截得的弦长等于
轴截得的弦长等于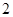 的圆的方程为__________________.
的圆的方程为__________________.