题目内容
(本小题满分12分)
在数列 中,已知
中,已知 ,
, ,
,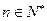 .
.
(1)证明数列 为等比数列,并求数列
为等比数列,并求数列 的通项公式;
的通项公式;
(2)求证: ,
,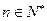 .
.
在数列
 中,已知
中,已知 ,
, ,
,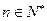 .
.(1)证明数列
 为等比数列,并求数列
为等比数列,并求数列 的通项公式;
的通项公式;(2)求证:
 ,
,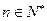 .
.略
(1)注意到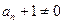 ,所以原式整理得:
,所以原式整理得: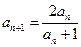
由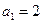 ,
,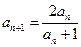 得对
得对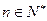 ,
,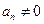 .从而由
.从而由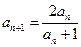 ,两边取倒数得:
,两边取倒数得: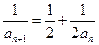 …………………………2分
…………………………2分
,即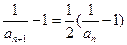
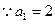 ,
,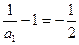
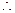 数列
数列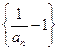 是首项为
是首项为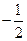 ,公比为
,公比为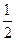 的等比数列
的等比数列 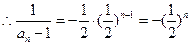
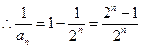 .
.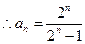 故数列
故数列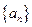 的通项公式是
的通项公式是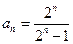 .
.
…………………………………4分
(2)证法1: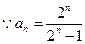 ,
,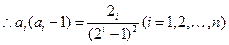 当
当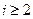 时,
时,

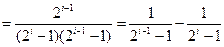 ……8分
……8分
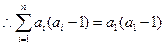
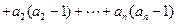
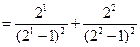 +
+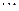
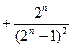
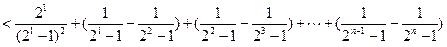
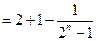
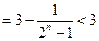 .…………………………………………………………12分
.…………………………………………………………12分
证法2: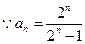 ,
,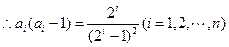 当
当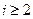 时,
时,
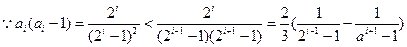 ………………8分
………………8分
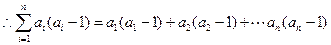
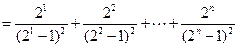
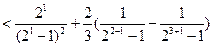
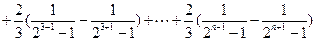
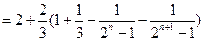
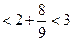 .………………………………………………………………………………12分
.………………………………………………………………………………12分
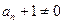 ,所以原式整理得:
,所以原式整理得: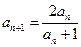
由
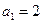 ,
,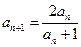 得对
得对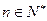 ,
,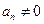 .从而由
.从而由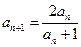 ,两边取倒数得:
,两边取倒数得: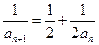 …………………………2分
…………………………2分,即
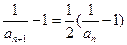
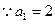 ,
,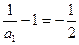
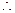 数列
数列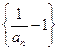 是首项为
是首项为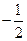 ,公比为
,公比为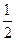 的等比数列
的等比数列 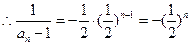
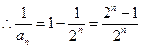 .
.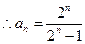 故数列
故数列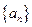 的通项公式是
的通项公式是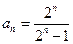 .
.…………………………………4分
(2)证法1:
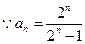 ,
,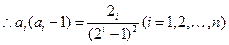 当
当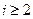 时,
时,
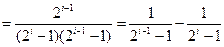 ……8分
……8分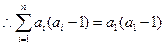
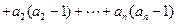
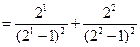 +
+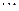
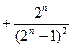
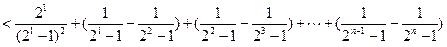
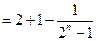
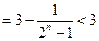 .…………………………………………………………12分
.…………………………………………………………12分证法2:
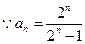 ,
,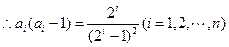 当
当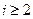 时,
时,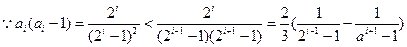 ………………8分
………………8分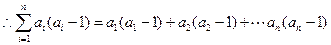
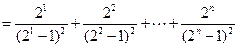
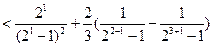
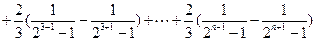
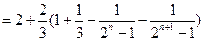
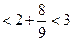 .………………………………………………………………………………12分
.………………………………………………………………………………12分
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
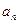 }是公差不为零的等差数列,
}是公差不为零的等差数列,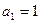 ,且
,且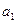 ,
,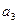 ,
,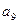 成等比数列.
成等比数列.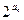 }的前n项和
}的前n项和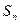 .
.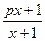 确定数列{an}的自反数列为{bn},求an;
确定数列{an}的自反数列为{bn},求an;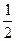 (cn+
(cn+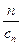 ).写出Sn表达式,并证明你的结论;
).写出Sn表达式,并证明你的结论;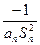 ,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.
,Dn是数列{dn}的前n项之和,且Dn>log a (1-2a)恒成立,求a的取值范围.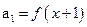 ,
,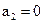 ,
,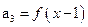 ,其中
,其中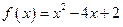 ,数列{an}前n项和存在最小值。
,数列{an}前n项和存在最小值。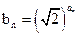 ,求数列
,求数列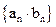 的前n项和
的前n项和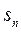
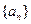 的前
的前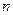 项和为
项和为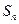 ,已知
,已知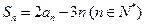 .
. ;
;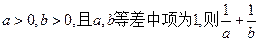 的最小值为( )
的最小值为( )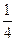
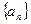 中,
中,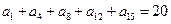 ,则
,则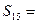 .
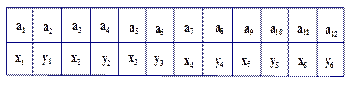
.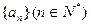 前12项,如下表所示:
前12项,如下表所示:
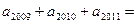
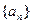 中,
中,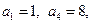 则
则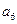 =
=