题目内容
(本小题满分14分)设数列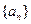 的前
的前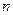 项和为
项和为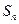 ,已知
,已知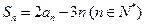 .
.
(1)求数列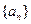 的通项公式
的通项公式 ;
;
(2)问数列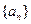 中是否存在某三项,它们可以构成一个等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
中是否存在某三项,它们可以构成一个等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
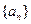 的前
的前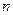 项和为
项和为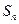 ,已知
,已知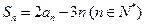 .
.(1)求数列
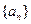 的通项公式
的通项公式 ;
;(2)问数列
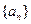 中是否存在某三项,它们可以构成一个等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.
中是否存在某三项,它们可以构成一个等差数列?若存在,请求出一组适合条件的项;若不存在,请说明理由.(1)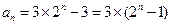
(2)数列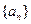 中不存在某三项,使它们可以构成一个等差数列
中不存在某三项,使它们可以构成一个等差数列
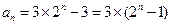
(2)数列
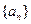 中不存在某三项,使它们可以构成一个等差数列
中不存在某三项,使它们可以构成一个等差数列(1)当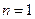 时,
时,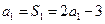 ,所以
,所以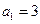 …………1分
…………1分
当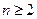 时,由
时,由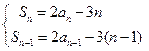 ,两式相减得
,两式相减得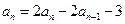 ,…3分
,…3分
即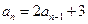 ,所以
,所以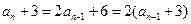 ,即
,即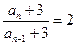 , …4分
, …4分
又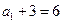 ,所以数列
,所以数列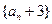 是以
是以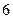 为首项,以
为首项,以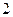 为公比的等比数列. ……5分
为公比的等比数列. ……5分
(2)由(1)知,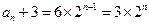 ,所以
,所以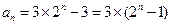 . ……7分
. ……7分
假设存在某三项,不妨设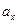 ,
,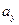 ,
,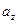 三项成等差数列,其中
三项成等差数列,其中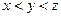 ,
,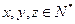 ,
,
则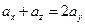 , ……………9分
, ……………9分
即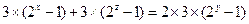 ,所以
,所以 ,
,
等式两边同除以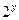 ,得
,得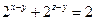 , …………11分
, …………11分
因为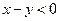 ,
,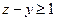 ,所以
,所以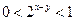 ,
,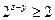 , …………13分
, …………13分
所以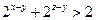 ,这与
,这与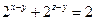 矛盾.
矛盾.
假设不存在,故数列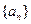 中不存在某三项,使它们可以构成一个等差数列.…14分
中不存在某三项,使它们可以构成一个等差数列.…14分
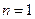 时,
时,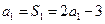 ,所以
,所以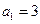 …………1分
…………1分当
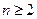 时,由
时,由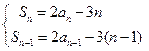 ,两式相减得
,两式相减得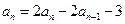 ,…3分
,…3分即
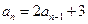 ,所以
,所以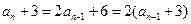 ,即
,即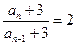 , …4分
, …4分又
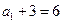 ,所以数列
,所以数列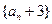 是以
是以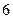 为首项,以
为首项,以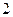 为公比的等比数列. ……5分
为公比的等比数列. ……5分(2)由(1)知,
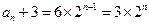 ,所以
,所以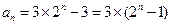 . ……7分
. ……7分假设存在某三项,不妨设
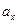 ,
,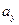 ,
,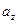 三项成等差数列,其中
三项成等差数列,其中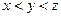 ,
,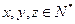 ,
,则
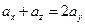 , ……………9分
, ……………9分即
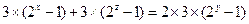 ,所以
,所以 ,
,等式两边同除以
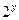 ,得
,得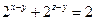 , …………11分
, …………11分因为
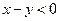 ,
,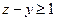 ,所以
,所以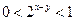 ,
,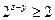 , …………13分
, …………13分所以
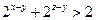 ,这与
,这与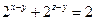 矛盾.
矛盾.假设不存在,故数列
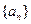 中不存在某三项,使它们可以构成一个等差数列.…14分
中不存在某三项,使它们可以构成一个等差数列.…14分
练习册系列答案
相关题目
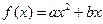 经过点(1,1),
经过点(1,1),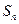 为数列
为数列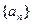 的前n项和,点
的前n项和,点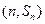 (
(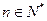 )在曲线
)在曲线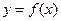 上.
上.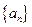 的通项公式
的通项公式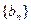 的第n项
的第n项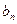 是数列
是数列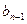 项(
项(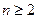 ),且
),且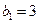 .
.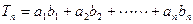
 中,已知
中,已知 ,
, ,
,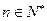 .
. 为等比数列,并求数列
为等比数列,并求数列 ,
,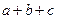 的值为 ( )
的值为 ( )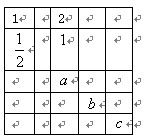
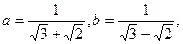 则
则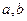 的等差中项为( )
的等差中项为( )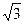
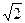
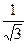
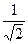
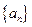 中,
中,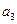 +
+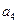 +
+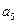 =12,那么
=12,那么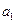 +
+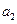 +…+
+…+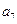 =( )
=( )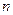 项和为
项和为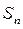 ,若
,若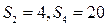 ,则该数列的公差
,则该数列的公差 __________
__________ _
_ __
__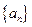 中,
中,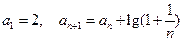 ,则
,则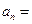 ( )
( )