题目内容
【题目】在平面直角坐标系
中，曲线C的参数方程为
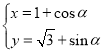（α为参数）.以坐标原点O为极点，x轴的正半轴为极轴建立极坐标系，直线l的极坐标方程为
，（
）.
（1）求曲线C的极坐标方程；
（2）设直线l与曲线C相交于不同的两点
，
，指出
的范围，并求
的取值范围.
【答案】（1）
；（2）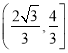
.
【解析】
(1)消去参数
即可得曲线C的直角坐标方程,再利用
及
代入化简即可.
(2)根据直线与圆的位置关系可得
,再根据极坐标的几何意义将
代入曲线
的极坐标方程,化简根据韦达定理以及辅助角公式求解即可.
（1）将曲线C的参数方程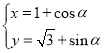
,消去参数,
得
.
将及代入上式,
得.
（2）依题意,因为圆心
到极点的倾斜角为
,
过极点圆的切线和极点与圆心连线的直线夹角为
，
故，将代入曲线的极坐标方程,
得
.
设
,
,则
,
.
所以
.
因为,所以
,
则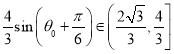
,
所以
的取值范围为.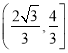
【题目】当今世界科技迅猛发展，信息日新月异．为增强全民科技意识，提高公众科学素养，某市图书馆开展了以“亲近科技、畅想未来”为主题的系列活动，并对不同年龄借阅者对科技类图书的情况进行了调查．该图书馆从只借阅了一本图书的借阅者中随机抽取100名，数据统计如表：
借阅科技类图书（人） | 借阅非科技类图书（人） | |
年龄不超过50岁 | 20 | 25 |
年龄大于50岁 | 10 | 45 |
（1）是否有99%的把握认为年龄与借阅科技类图书有关？
（2）该图书馆为了鼓励市民借阅科技类图书，规定市民每借阅一本科技类图书奖励积分2分，每借阅一本非科技类图书奖励积分1分，积分累计一定数量可以用积分换购自己喜爱的图书．用表中的样本频率作为概率的估计值．
（i）现有3名借阅者每人借阅一本图书，记此3人增加的积分总和为随机变量ξ，求ξ的分布列和数学期望；
（ii）现从只借阅一本图书的借阅者中选取16人，则借阅科技类图书最有可能的人数是多少？
附：K2
，其中n＝a+b+c+d．
P（K2≥k） | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.635 | 10.828 |
