题目内容
数列{an}满足a1=2,对于任意的n∈N*都有an>0,且(n+1)an2+an·an+1-nan+12=0,又知数列{bn}的通项为bn=2n-1+1.
(1)求数列{an}的通项an及它的前n项和Sn;
(2)求数列{bn}的前n项和Tn;
(3)猜想Sn与Tn的大小关系,并说明理由.
(1)求数列{an}的通项an及它的前n项和Sn;
(2)求数列{bn}的前n项和Tn;
(3)猜想Sn与Tn的大小关系,并说明理由.
(1) Sn=n2+n,(2) Tn=2n+n-1 (3)猜想当n≥5时,Tn>Sn,即2n>n2+1
(1)可解得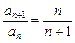 ,从而an=2n,有Sn=n2+n,
,从而an=2n,有Sn=n2+n,
(2)Tn=2n+n-1.
(3)Tn-Sn=2n-n2-1,验证可知,n=1时,T1=S1,n=2时T2<S2;n=3时,T3<S3;n=4时,T4<S4;n=5时,T5>S5;n=6时T6>S6
猜想当n≥5时,Tn>Sn,即2n>n2+1
可用数学归纳法证明(略).
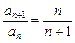 ,从而an=2n,有Sn=n2+n,
,从而an=2n,有Sn=n2+n,(2)Tn=2n+n-1.
(3)Tn-Sn=2n-n2-1,验证可知,n=1时,T1=S1,n=2时T2<S2;n=3时,T3<S3;n=4时,T4<S4;n=5时,T5>S5;n=6时T6>S6
猜想当n≥5时,Tn>Sn,即2n>n2+1
可用数学归纳法证明(略).

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目
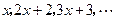 为等比数列,求这个数列的第
为等比数列,求这个数列的第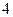 项.
项.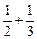 +…+
+…+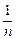 ,(n∈N*),设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式:
,(n∈N*),设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式: 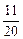 [log(m-1)m]2恒成立.
[log(m-1)m]2恒成立. 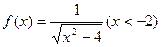 .(Ⅰ) 求f –1(x);(Ⅱ) 若数列{an}的首项为a1=1,
.(Ⅰ) 求f –1(x);(Ⅱ) 若数列{an}的首项为a1=1,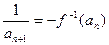 (nÎN+),求{an}的通项公式an;(Ⅲ) 设bn=an+12+an+22+¼+a2n+12,是否存在最小的正整数k,使对于任意nÎN+有bn<
(nÎN+),求{an}的通项公式an;(Ⅲ) 设bn=an+12+an+22+¼+a2n+12,是否存在最小的正整数k,使对于任意nÎN+有bn<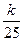 成立.若存在,求出k的值;若不存在,说明理由.
成立.若存在,求出k的值;若不存在,说明理由.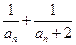 ,数列{bn}的前n项和为Sn,求
,数列{bn}的前n项和为Sn,求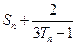 的值
的值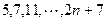 ,其中后一项比前一项大2.
,其中后一项比前一项大2.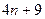 是否为此数列的项?
是否为此数列的项?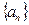 中,
中,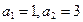 ,且
,且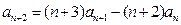 ,(n∈N*),求通项公式
,(n∈N*),求通项公式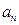 .
.