题目内容
已知a1=2,点(an,an+1)在函数f(x)=x2+2x的图象上,其中n=1,2,3,…
(1)证明:数列{lg(1+an) }是等比数列.
(2)设Tn=(1+a1)(1+a2)…(1+an),求Tn及数列{an}的通项.
(3)记bn=
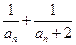 ,数列{bn}的前n项和为Sn,求
,数列{bn}的前n项和为Sn,求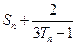 的值
的值Tn=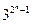 ,
,

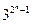 ,
,

解:(1)由已知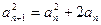
∴ ……………………………………….2分
……………………………………….2分
∵a1=2
∴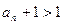 两边取对数得
两边取对数得 ……….3分
……….3分
即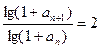 ∴
∴ 是公比为2的等比数列 …..4分
是公比为2的等比数列 …..4分
(2)由(1)知
∴ ………………………………..7分
………………………………..7分
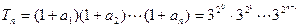
 ………………………………………..10分
………………………………………..10分
(3)∵
∴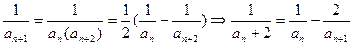 ….13分
….13分
又 ………..14分
………..14分
∴
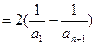 …………………………………………….16分
…………………………………………….16分
∵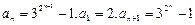 ∴
∴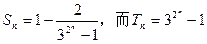
∴ ………………………18分
………………………18分
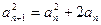
∴
 ……………………………………….2分
……………………………………….2分∵a1=2
∴
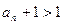 两边取对数得
两边取对数得 ……….3分
……….3分即
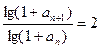 ∴
∴ 是公比为2的等比数列 …..4分
是公比为2的等比数列 …..4分(2)由(1)知

∴
 ………………………………..7分
………………………………..7分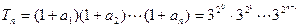
 ………………………………………..10分
………………………………………..10分(3)∵

∴
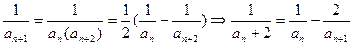 ….13分
….13分又
 ………..14分
………..14分∴

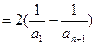 …………………………………………….16分
…………………………………………….16分∵
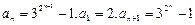 ∴
∴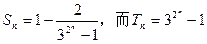
∴
 ………………………18分
………………………18分
练习册系列答案
相关题目
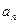 }满足
}满足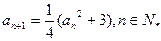 。
。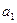 为奇数,则对一切
为奇数,则对一切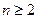 ,
,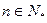 ,都有
,都有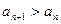 ,求
,求 }的前n项和为
}的前n项和为 对任意
对任意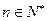 ,
, 。(Ⅰ)求数列
。(Ⅰ)求数列 是递增数列,求实数m的取值范围。
是递增数列,求实数m的取值范围。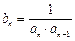 ,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.
,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.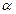 为锐角,且
为锐角,且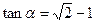 ,
,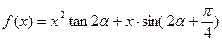 ,数列{an}的首项
,数列{an}的首项 .
.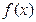 的表达式;
的表达式;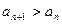 ;
; 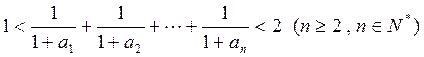
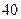 %,从2009年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化.
%,从2009年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化. 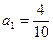 ,经过
,经过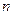 年后绿化的面积为
年后绿化的面积为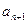 ,试用
,试用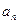 表示
表示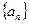 的第
的第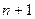 项
项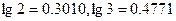 )
)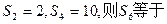
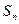 为等差数列
为等差数列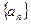 的前
的前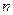 项和,
项和,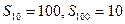 ,求
,求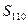 .
.