题目内容
已知Sn=1+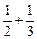 +…+
+…+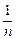 ,(n∈N*),设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式:
,(n∈N*),设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式:
f(n)>[logm(m-1)]2-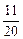 [log(m-1)m]2恒成立.
[log(m-1)m]2恒成立.
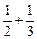 +…+
+…+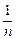 ,(n∈N*),设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式:
,(n∈N*),设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式: f(n)>[logm(m-1)]2-
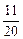 [log(m-1)m]2恒成立.
[log(m-1)m]2恒成立. ∵Sn=1+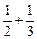 +…+
+…+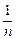 . (n∈N*)
. (n∈N*)
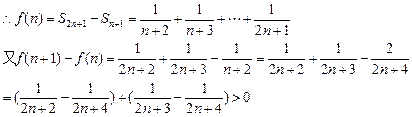
∴f(n+1)>f(n)
∴f(n)是关于n的增函数
∴f(n) min=f(2)=
∴要使一切大于1的自然数n,不等式
f(n)>[logm(m-1)]2-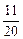 [log(m-1)m]2恒成立
[log(m-1)m]2恒成立
只要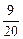 >[logm(m-1)]2-
>[logm(m-1)]2-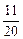 [log(m-1)m]2成立即可
[log(m-1)m]2成立即可
由 得m>1且m≠2
得m>1且m≠2
此时设[logm(m-1)]2=t 则t>0
于是 解得0<t<1
解得0<t<1
由此得0<[logm(m-1)]2<1
解得m>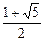 且m≠2.
且m≠2.
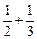 +…+
+…+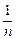 . (n∈N*)
. (n∈N*)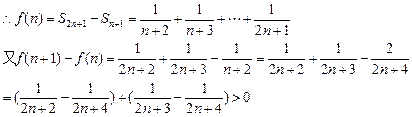
∴f(n+1)>f(n)
∴f(n)是关于n的增函数
∴f(n) min=f(2)=

∴要使一切大于1的自然数n,不等式
f(n)>[logm(m-1)]2-
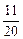 [log(m-1)m]2恒成立
[log(m-1)m]2恒成立只要
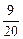 >[logm(m-1)]2-
>[logm(m-1)]2-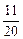 [log(m-1)m]2成立即可
[log(m-1)m]2成立即可由
 得m>1且m≠2
得m>1且m≠2此时设[logm(m-1)]2=t 则t>0
于是
 解得0<t<1
解得0<t<1由此得0<[logm(m-1)]2<1
解得m>
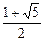 且m≠2.
且m≠2.
练习册系列答案
相关题目
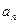 }满足
}满足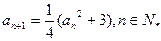 。
。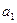 为奇数,则对一切
为奇数,则对一切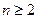 ,
,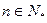 ,都有
,都有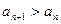 ,求
,求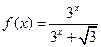 上两点
上两点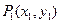 、
、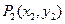 ,若
,若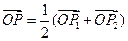 ,且
,且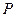 点的横坐标为
点的横坐标为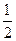
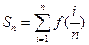 ,
,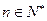 ,求
,求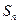 ;
;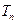 为数列
为数列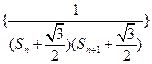 的前
的前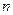 项和,若
项和,若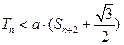 对一切
对一切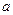 的取值范围。
的取值范围。 }的前n项和为
}的前n项和为 对任意
对任意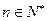 ,
, 。(Ⅰ)求数列
。(Ⅰ)求数列 是递增数列,求实数m的取值范围。
是递增数列,求实数m的取值范围。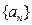 满足性质:对于
满足性质:对于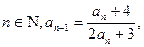 且
且 求
求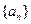 满足:
满足: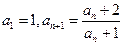
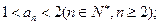
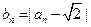
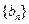 是递减数列;(2)设
是递减数列;(2)设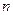 项和为
项和为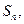 求证:
求证: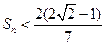
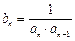 ,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.
,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.