题目内容
已知数列{an}的前n项Sn=pn+q(p≠0,p≠1),求数列{an}是等比数列的充要条件.
证明略
a1=S1=p+q
当n≥2时,an=Sn-Sn-1=pn-1(p-1)
∵p≠0,p≠1,∴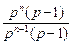 =p
=p
若{an}为等比数列,则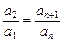 =p
=p
∴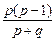 =p,
=p,
∵p≠0,∴p-1=p+q,∴q=-1
这是{an}为等比数列的必要条件.
下面证明q=-1是{an}为等比数列的充分条件
当q=-1时,∴Sn=pn-1(p≠0,p≠1),a1=S1=p-1
当n≥2时,an=Sn-Sn-1=pn-pn-1=pn-1(p-1)
∴an=(p-1)pn-1 (p≠0,p≠1)
 =p为常数
=p为常数
∴q=-1时,数列{an}为等比数列 即数列{an}是等比数列的充要条件为q=-1.
即数列{an}是等比数列的充要条件为q=-1.

当n≥2时,an=Sn-Sn-1=pn-1(p-1)
∵p≠0,p≠1,∴
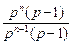 =p
=p若{an}为等比数列,则
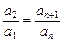 =p
=p∴
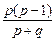 =p,
=p,∵p≠0,∴p-1=p+q,∴q=-1
这是{an}为等比数列的必要条件.
下面证明q=-1是{an}为等比数列的充分条件

当q=-1时,∴Sn=pn-1(p≠0,p≠1),a1=S1=p-1
当n≥2时,an=Sn-Sn-1=pn-pn-1=pn-1(p-1)
∴an=(p-1)pn-1 (p≠0,p≠1)
 =p为常数
=p为常数∴q=-1时,数列{an}为等比数列
 即数列{an}是等比数列的充要条件为q=-1.
即数列{an}是等比数列的充要条件为q=-1.
练习册系列答案
相关题目
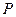 从原点出发,沿
从原点出发,沿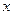 轴正向移动距离
轴正向移动距离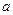 到达
到达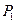 ,再沿
,再沿 轴正向移动距离
轴正向移动距离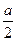 点,到达
点,到达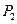 点,再沿
点,再沿 到达
到达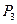 点,
点,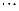 依次类推无限进行每转1次距离缩小一半.
依次类推无限进行每转1次距离缩小一半.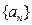 满足性质:对于
满足性质:对于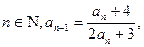 且
且 求
求 “2001年国内生产总值达到95933亿元,比上年增长7
“2001年国内生产总值达到95933亿元,比上年增长7 3%,”如果“十·五”期间(2001年~2005年)每年的国内生产总值都按此年增长率增长,那么到“十·五”末我国国内年生产总值约为_________亿元.
3%,”如果“十·五”期间(2001年~2005年)每年的国内生产总值都按此年增长率增长,那么到“十·五”末我国国内年生产总值约为_________亿元.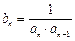 ,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.
,其前n项和为Sn.(1)求数列{an}的通项公式an;(2)若S2为S1,Sm(m∈N*)的等比中项,求正整数m的值.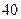 %,从2009年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化.
%,从2009年开始,计划每年将非绿化面积的8%绿化,由于修路和盖房等用地,原有绿化面积的2%被非绿化. 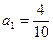 ,经过
,经过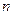 年后绿化的面积为
年后绿化的面积为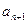 ,试用
,试用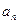 表示
表示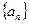 的第
的第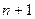 项
项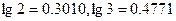 )
) 中,
中,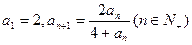 ,求数列
,求数列