题目内容
14.已知点F是椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左焦点,点P为椭圆C上任意一点,点Q的坐标为(4,3),则|PQ|+|PF|的最大值为5$\sqrt{2}$.分析 设椭圆C的右焦点为F′(1,0),由已知条件推导出|PQ|+|PF|=|PQ|+2$\sqrt{2}$-|PF′|,利用Q,F′,P共线
,可得|PQ|+|PF|取最大值.
解答 解:∵点F为椭圆C:$\frac{{x}^{2}}{2}$+y2=1的左焦点,∴F(-1,0),
∵点P为椭圆C上任意一点,点Q的坐标为(4,3),
设椭圆C的右焦点为F′(1,0),
∴|PQ|+|PF|=|PQ|+2$\sqrt{2}$-|PF′|
=2$\sqrt{2}$+|PQ|-|PF′|,
∵|PQ|-|PF′|≤|QF′|=3$\sqrt{2}$,
∴|PQ|+|PF|≤5$\sqrt{2}$,即最大值为5$\sqrt{2}$,此时Q,F′,P共线
故答案为:5$\sqrt{2}$.
点评 本题考查椭圆的方程与性质,考查学生转化问题的能力,正确转化是关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
4.不等式(x2-1)(x+1)≤0的解集为( )
| A. | (-∞,-1] | B. | (-∞,-1) | C. | (-∞,1) | D. | (-∞,1] |
2.已知点 F 是抛物线 y2=4x的焦点,M、N 是该抛物线上两点,|MF|+|NF|=6,则 MN中点的横坐标为( )
| A. | $\frac{3}{2}$ | B. | 2 | C. | $\frac{5}{2}$ | D. | 3 |
9.已知复数z满足方程$\frac{z+i}{z}$=i(i为虚数单位),则$\overline{z}$=( )
| A. | $\frac{1}{2}$+$\frac{1}{2}$i | B. | $\frac{1}{2}$-$\frac{1}{2}$i | C. | -$\frac{1}{2}$+$\frac{1}{2}$i | D. | -$\frac{1}{2}$-$\frac{1}{2}$i |
19.若某几何体的三视图如图所示,则此几何体的体积等于( )


| A. | 24 | B. | 30 | C. | 10 | D. | 60 |
4.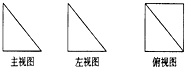 如图,是一个空间几何体的主视图(正视图)、左视图、俯视图,如果图中直角三角形的直角边长均为1,那么这个几何体的侧面积为( )
如图,是一个空间几何体的主视图(正视图)、左视图、俯视图,如果图中直角三角形的直角边长均为1,那么这个几何体的侧面积为( )
 如图,是一个空间几何体的主视图(正视图)、左视图、俯视图,如果图中直角三角形的直角边长均为1,那么这个几何体的侧面积为( )
如图,是一个空间几何体的主视图(正视图)、左视图、俯视图,如果图中直角三角形的直角边长均为1,那么这个几何体的侧面积为( )| A. | 1+$\sqrt{2}$ | B. | 2+$\sqrt{2}$ | C. | 1+2$\sqrt{2}$ | D. | 2+2$\sqrt{2}$ |