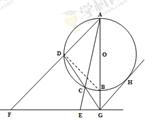
题目内容
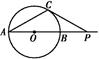
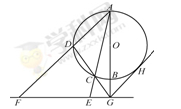
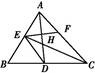
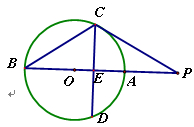
如图, 是圆
是圆 的直径,
的直径, 是
是 延长线上的一点,
延长线上的一点,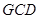 是圆
是圆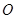 的割线,过点
的割线,过点 作
作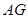 的垂线,交直线
的垂线,交直线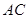 于点
于点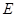 ,交直线
,交直线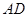 于点
于点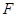 ,过点
,过点 作圆
作圆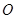 的切线,切点为
的切线,切点为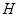 .
.
(1)求证: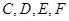 四点共圆;(2)若
四点共圆;(2)若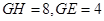 ,求
,求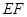 的长.
的长.
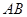 是圆
是圆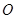 的直径,
的直径, 是
是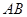 延长线上的一点,
延长线上的一点,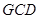 是圆
是圆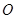 的割线,过点
的割线,过点 作
作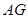 的垂线,交直线
的垂线,交直线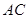 于点
于点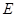 ,交直线
,交直线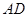 于点
于点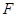 ,过点
,过点 作圆
作圆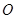 的切线,切点为
的切线,切点为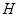 .
.
(1)求证:
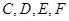 四点共圆;(2)若
四点共圆;(2)若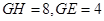 ,求
,求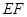 的长.
的长.(1)详见解析;(2)12
试题分析:(1)根据四边形的外角等于内角的对角时四点共圆,证
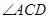
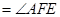 问题即可得证。(2)由(1)可知
问题即可得证。(2)由(1)可知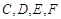 四点共圆,则可根据切割弦定理求边长。
四点共圆,则可根据切割弦定理求边长。试题解析:(1)
证明:连结
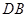 ,∵
,∵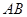 是圆
是圆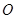 的直径,
的直径,∴
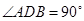 ,
,在
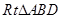 和
和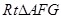 中,
中,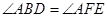
又∵
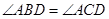 ∴
∴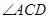
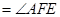
∴
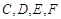 四点共圆。
四点共圆。(2)∵
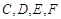 四点共圆,∴
四点共圆,∴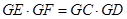
∵
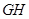 是圆
是圆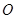 的切线,∴
的切线,∴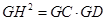 ∴
∴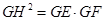
又因为
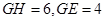 ∴
∴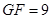
∴
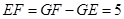

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目

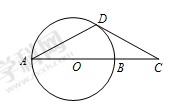
 是圆
是圆 的直径,延长
的直径,延长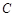 ,使
,使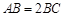 ,且
,且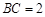 ,
,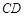 是圆
是圆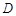 ,连接
,连接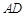 ,则
,则 ________,
________,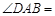 ________.
________.
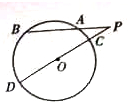
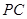 与圆
与圆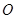 相切于
相切于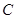 ,割线
,割线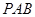 经过圆心
经过圆心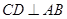 于点
于点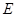 ,
,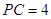 ,
,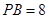 ,则
,则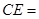 ___.
___.
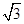 ,若∠CAP=30°,则PB= .
,若∠CAP=30°,则PB= .