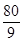题目内容
如图所示,AB是☉O的直径,P是AB延长线上的一点,过P作☉O的切线,切点为C,PC=2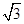 ,若∠CAP=30°,则PB= .
,若∠CAP=30°,则PB= .
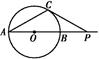
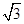 ,若∠CAP=30°,则PB= .
,若∠CAP=30°,则PB= . 
2
连接OC,因为PC=2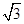 ,∠CAP=30°,
,∠CAP=30°,
所以OC=2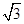 tan 30°=2,则AB=2OC=4,
tan 30°=2,则AB=2OC=4,
由切割线定理得PC2=PB·PA=PB·(PB+BA),
解得PB=2.
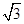 ,∠CAP=30°,
,∠CAP=30°,所以OC=2
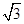 tan 30°=2,则AB=2OC=4,
tan 30°=2,则AB=2OC=4,由切割线定理得PC2=PB·PA=PB·(PB+BA),
解得PB=2.

练习册系列答案
相关题目
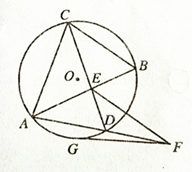
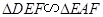 ;(2)EF//CB.
;(2)EF//CB.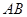 是圆
是圆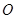 的直径,
的直径, 是
是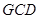 是圆
是圆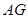 的垂线,交直线
的垂线,交直线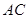 于点
于点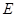 ,交直线
,交直线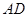 于点
于点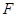 ,过点
,过点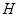 .
.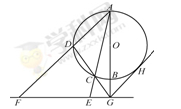
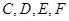 四点共圆;(2)若
四点共圆;(2)若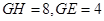 ,求
,求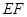 的长.
的长.

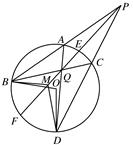
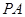 是⊙
是⊙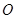 的切线,
的切线,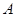 是切点,直线
是切点,直线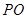 交⊙
交⊙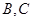 两点,
两点,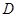 是
是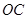 的中点,连接
的中点,连接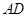 并延长交⊙
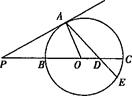
并延长交⊙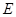 ,若
,若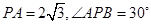 ,则
,则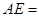 .
.
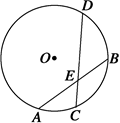
 是圆
是圆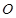 的切线,切点为点
的切线,切点为点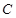 ,直线
,直线 与圆
与圆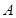 、
、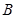 两点,
两点,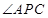 的角平分线交弦
的角平分线交弦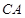 、
、 于
于 、
、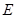 两点,已知
两点,已知 ,
, ,则
,则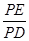 的值为 .
的值为 .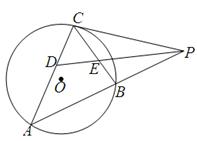
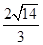 B.
B.
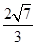 D.
D.