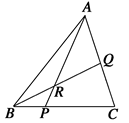
题目内容
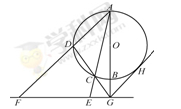
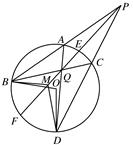
如图,D,E分别为△ABC边AB,AC的中点,直线DE交△ABC的外接圆于F,G两点,若CF∥AB,证明:
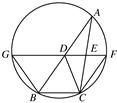
(1)CD=BC;
(2)△BCD∽△GBD.

(1)CD=BC;
(2)△BCD∽△GBD.
(1)见解析(2)见解析
(1)因为D,E分别为AB,AC的中点,所以DE∥BC.
又已知CF∥AB,故四边形BCFD是平行四边形,所以CF=BD=AD.
而CF∥AD,连结AF,
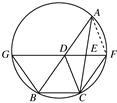
所以四边形ADCF是平行四边形,
故CD=AF.
因为CF∥AB,所以BC=AF,故CD=BC.
(2)因为FG∥BC,故GB=CF.
由(1)可知BD=CF,所以GB=BD.
所以∠BGD=∠BDG.
而∠DGB=∠EFC=∠DBC,由(1)知CD=BC,
故△BCD∽△GBD.
又已知CF∥AB,故四边形BCFD是平行四边形,所以CF=BD=AD.
而CF∥AD,连结AF,

所以四边形ADCF是平行四边形,
故CD=AF.
因为CF∥AB,所以BC=AF,故CD=BC.
(2)因为FG∥BC,故GB=CF.
由(1)可知BD=CF,所以GB=BD.
所以∠BGD=∠BDG.
而∠DGB=∠EFC=∠DBC,由(1)知CD=BC,
故△BCD∽△GBD.

练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
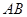 是圆
是圆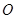 的直径,
的直径, 是
是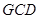 是圆
是圆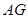 的垂线,交直线
的垂线,交直线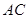 于点
于点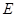 ,交直线
,交直线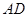 于点
于点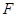 ,过点
,过点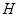 .
.
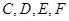 四点共圆;(2)若
四点共圆;(2)若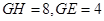 ,求
,求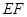 的长.
的长.
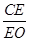 的值为________.
的值为________.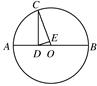
 是圆
是圆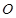 的切线,切点为点
的切线,切点为点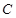 ,直线
,直线 与圆
与圆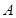 、
、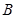 两点,
两点,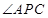 的角平分线交弦
的角平分线交弦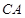 、
、 于
于 、
、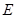 两点,已知
两点,已知 ,
, ,则
,则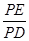 的值为 .
的值为 .
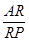 等于
等于