题目内容
如图,已知△ABC中的两条角平分线AD和CE相交于H,∠B=60°,F在AC上,且AE=AF.
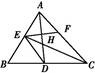
(1)证明:B,D,H,E四点共圆;
(2)证明:CE平分∠DEF.

(1)证明:B,D,H,E四点共圆;
(2)证明:CE平分∠DEF.
证明见解析
证明:(1)在△ABC中,∵∠B=60°,
∴∠BAC+∠BCA=120°.
∵AD,CE是角平分线,
∴∠HAC+∠HCA=60°,∴∠AHC=120°.
∴∠EHD=∠AHC=120°.
∵∠EBD+∠EHD=180°,
∴B,D,H,E四点共圆.
(2)如图所示,连结BH,
则BH为∠ABC的平分线,
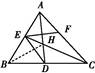
得∠HBD=30°.
由(1)知B,D,H,E四点共圆,
∴∠CED=∠HBD=30°.
又∠AEH=∠EBD=60°,AE=AF,AH平分∠EAF,
∴EF⊥AD.可得∠CEF=30°.
∴CE平分∠DEF.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
 是圆
是圆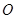 的直径,
的直径, 是
是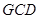 是圆
是圆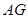 的垂线,交直线
的垂线,交直线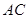 于点
于点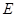 ,交直线
,交直线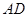 于点
于点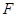 ,过点
,过点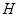 .
.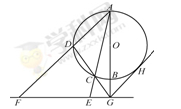
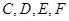 四点共圆;(2)若
四点共圆;(2)若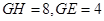 ,求
,求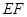 的长.
的长.
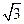 ,延长CE交AB于点F,求△BCF外接圆的半径.
,延长CE交AB于点F,求△BCF外接圆的半径.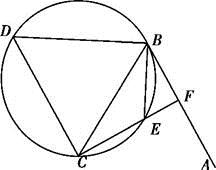
 是半圆的直径,
是半圆的直径,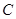 是
是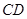 切半圆于点
切半圆于点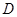 ,
,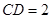 ,
,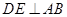 ,垂足为
,垂足为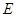 ,且
,且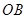 的中点,则
的中点,则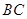 的长为 .
的长为 .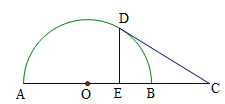
 ,则圆O的半径OC的长为 .
,则圆O的半径OC的长为 .
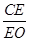 的值为________.
的值为________.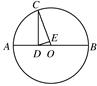
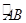 于点E,连接EC,则∠OEC=( ).
于点E,连接EC,则∠OEC=( ).