题目内容
【题目】已知复数
满足
，
的虚部为
，且在复平面内对应的点在第二象限.
（1）求复数；
（2）若复数
满足
，求在复平面内对应的点的集合构成图形的面积.
【答案】（1）
；（2）
【解析】
（1）设出复数
，利用已知列出方程组，求解可得复数； （2）把复数
代入
，利用复数代数形式的乘除运算化简，由复数求模公式计算
，由复数
满足
，由复数的几何意义得出在复平面内对应的点的集合构成图形是什么，从而计算出对应面积.
(1)设z=x+yi(x,y∈R),则z2=x2-y2+2xyi,
由|z|=
,z2的虚部为-2,且z在复平面内对应的点在第二象限,
得
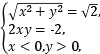解得
∴z=-1+i.
(2)由(1)知,z=-1+i,
∴=
=
=
=-+i,
∴=
=
,
∴复数ω满足|ω-1|≤.
由复数的几何意义,得
ω在复平面内对应的点的集合构成的图形是以(1,0)为圆心,为半径的圆面,
∴其面积为π·
=
.
练习册系列答案
小学生10分钟口算测试100分系列答案
相关题目
【题目】为分析学生入学时的数学成绩对高一年级数学学习的影响，在高一年级学生中随机抽取10名学生，统计他们入学时的数学成绩和高一期末的数学成绩，如下表：
学生编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
入学成绩x(分) | 63 | 67 | 45 | 88 | 81 | 71 | 52 | 99 | 58 | 76 |
高一期末 成绩y(分) | 65 | 78 | 52 | 82 | 92 | 89 | 73 | 98 | 56 | 75 |
(1)求相关系数r；
(2)求y关于x的线性回归方程；
(3)若某学生入学时的数学成绩为80分，试估计他高一期末的数学成绩．
