题目内容
【题目】已知函数f(x)=ax2+bln x在x=1处有极值![]() .
.
(1)求a,b的值;
(2)求函数y=f(x)的单调性.
【答案】(1)![]() ;(2)见解析
;(2)见解析
【解析】
试题分析: (1)f′(x)=2ax+![]() .由题意可得:
.由题意可得: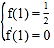 ,解得a,b.
,解得a,b.
(2)f(x)=![]() x2-lnx,f′(x)=x﹣
x2-lnx,f′(x)=x﹣![]() .函数定义域为(0,+∞).令f′(x)>0,f′(x)<0,分别解出即可得出单调区间.
.函数定义域为(0,+∞).令f′(x)>0,f′(x)<0,分别解出即可得出单调区间.
试题解析:
(1)∵f′(x)=2ax+![]() .又f(x)在x=1处有极值
.又f(x)在x=1处有极值![]() ,
,
∴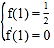 即
即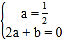 解得a=
解得a=![]() ,b=-1.
,b=-1.
(2)由(1)可知f(x)=![]() x2-lnx,其定义域是(0,+∞),
x2-lnx,其定义域是(0,+∞),
f′(x)=x-![]() =
=![]() .
.
由f′(x)<0,得0<x<1;由f′(x)>0,得x>1.
所以函数y=f(x)的单调减区间是(0,1),单调增区间是(1,+∞).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目