题目内容
对函数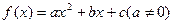 ,若存在
,若存在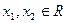 且
且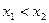 ,使得
,使得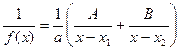 (其中A,B为常数),则称
(其中A,B为常数),则称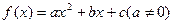 为“可分解函数”。
为“可分解函数”。
(1)试判断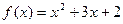 是否为“可分解函数”,若是,求出A,B的值;若不是,说明理由;
是否为“可分解函数”,若是,求出A,B的值;若不是,说明理由;
(2)用反证法证明: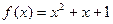 不是“可分解函数”;
不是“可分解函数”;
(3)若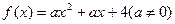 是“可分解函数”,则求a的取值范围,并写出A,B关于a的相应的表达式。
是“可分解函数”,则求a的取值范围,并写出A,B关于a的相应的表达式。
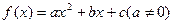 ,若存在
,若存在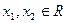 且
且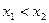 ,使得
,使得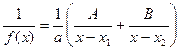 (其中A,B为常数),则称
(其中A,B为常数),则称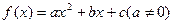 为“可分解函数”。
为“可分解函数”。(1)试判断
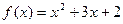 是否为“可分解函数”,若是,求出A,B的值;若不是,说明理由;
是否为“可分解函数”,若是,求出A,B的值;若不是,说明理由;(2)用反证法证明:
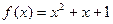 不是“可分解函数”;
不是“可分解函数”;(3)若
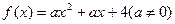 是“可分解函数”,则求a的取值范围,并写出A,B关于a的相应的表达式。
是“可分解函数”,则求a的取值范围,并写出A,B关于a的相应的表达式。原命题成立
(1)因为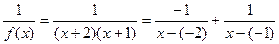 ,所以A= -1,B=1
,所以A= -1,B=1
(2)假设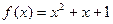 是“可分解函数”,即存在
是“可分解函数”,即存在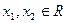 且
且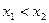 ,使得
,使得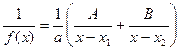 =
=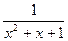
即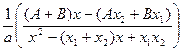 =
=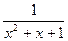 ,比较得:
,比较得:
方程组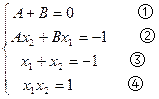 ,但联立方程③④无解,故方程组无解,所以假设不真,原命题成立。
,但联立方程③④无解,故方程组无解,所以假设不真,原命题成立。
(3)因为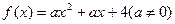 是“可分解函数”,所以
是“可分解函数”,所以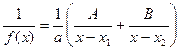
=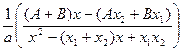 =
=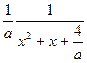
所以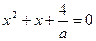 有两个不同的实根,所以
有两个不同的实根,所以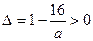
解得: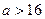 或
或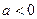
此时方程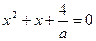 有两个不同的实根为
有两个不同的实根为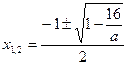 ,
,
且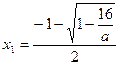 <
<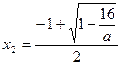 代入
代入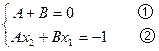 解得
解得
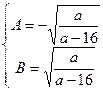
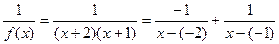 ,所以A= -1,B=1
,所以A= -1,B=1(2)假设
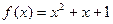 是“可分解函数”,即存在
是“可分解函数”,即存在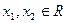 且
且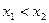 ,使得
,使得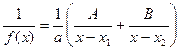 =
=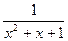
即
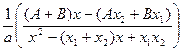 =
=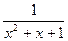 ,比较得:
,比较得:方程组
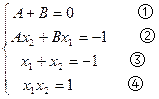 ,但联立方程③④无解,故方程组无解,所以假设不真,原命题成立。
,但联立方程③④无解,故方程组无解,所以假设不真,原命题成立。(3)因为
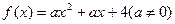 是“可分解函数”,所以
是“可分解函数”,所以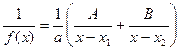
=
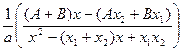 =
=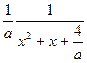
所以
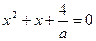 有两个不同的实根,所以
有两个不同的实根,所以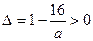
解得:
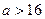 或
或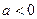
此时方程
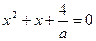 有两个不同的实根为
有两个不同的实根为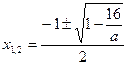 ,
,且
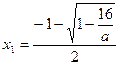 <
<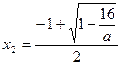 代入
代入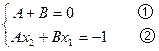 解得
解得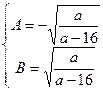

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
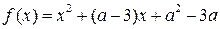 (a为常数).
(a为常数).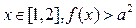 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;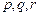 满足:
满足: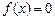 的两实根,判断①
的两实根,判断①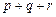 ,②
,②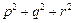 ,③
,③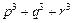 是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数
是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数 ,并求
,并求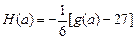 ,数列
,数列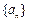 满足
满足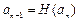
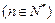 ,且
,且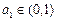 ,试判断
,试判断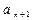 与
与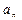 的大小,并证明.
的大小,并证明.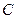 ,公路
,公路 恰好是
恰好是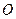 到
到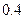 千米,城镇
千米,城镇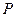 位于点
位于点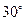 处,
处,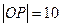 千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路
千米,现要在河岸边的某处修建一座码头,并修建两条公路,一条连接城镇,一条垂直连接公路 以便建立水陆交通网.
以便建立水陆交通网.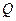 的位置),并求公路总长的最小值(精确到0.001千米)
的位置),并求公路总长的最小值(精确到0.001千米)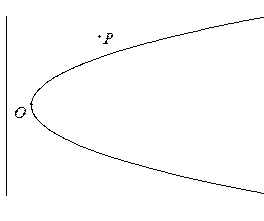
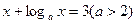 的解为
的解为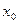 ,则
,则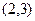
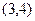
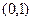
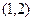
 分别是定义在R上的奇函数和偶函数,当
分别是定义在R上的奇函数和偶函数,当 时,
时, ,
, ,则不等式
,则不等式 的解集是
的解集是
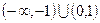


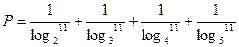 ,则
,则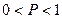
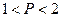
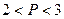
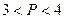
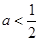 ,则
,则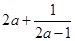 的最大值为 .
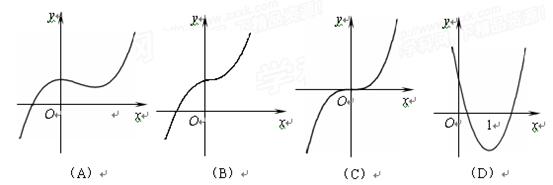
的最大值为 .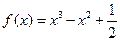 的图象大致是
的图象大致是