题目内容
本小题满分16分)已知函数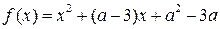 (a为常数).
(a为常数).
(Ⅰ)如果对任意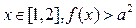 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;
(Ⅱ)设实数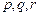 满足:
满足: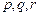 中的某一个数恰好等于a,且另两个恰为方程
中的某一个数恰好等于a,且另两个恰为方程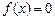 的两实根,判断①
的两实根,判断①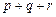 ,②
,②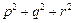 ,③
,③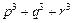 是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数
是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数 ,并求
,并求 的最小值;
的最小值;
(Ⅲ)对于(Ⅱ)中的 ,设
,设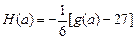 ,数列
,数列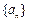 满足
满足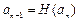
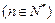 ,且
,且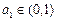 ,试判断
,试判断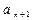 与
与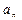 的大小,并证明.
的大小,并证明.
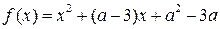 (a为常数).
(a为常数).(Ⅰ)如果对任意
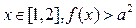 恒成立,求实数a的取值范围;
恒成立,求实数a的取值范围;(Ⅱ)设实数
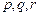 满足:
满足: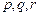 中的某一个数恰好等于a,且另两个恰为方程
中的某一个数恰好等于a,且另两个恰为方程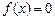 的两实根,判断①
的两实根,判断①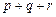 ,②
,②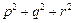 ,③
,③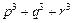 是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数
是否为定值?若是定值请求出:若不是定值,请把不是定值的表示为函数 ,并求
,并求 的最小值;
的最小值;(Ⅲ)对于(Ⅱ)中的
 ,设
,设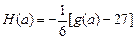 ,数列
,数列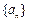 满足
满足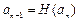
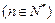 ,且
,且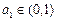 ,试判断
,试判断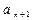 与
与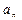 的大小,并证明.
的大小,并证明.(Ⅰ)a<-2(Ⅱ)同解析(Ⅲ)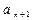 <
<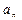
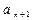 <
<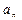
(Ⅰ)
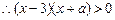 对
对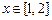 恒成立,
恒成立,
又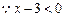 恒成立,
恒成立,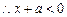 对
对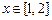 恒成立,
恒成立,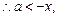 又
又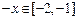 ,
,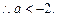 …
…
(Ⅱ)由 得:
得: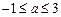 ,不妨设
,不妨设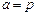 ,则q,r恰为方程两根,由韦达定理得:①
,则q,r恰为方程两根,由韦达定理得:①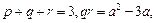
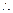 ②
②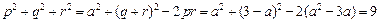
③而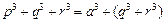
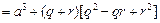

设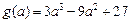 ,求导得:
,求导得: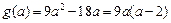
当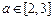 时,
时,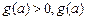 递增;当
递增;当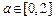 时,
时, 递减;
递减;
当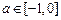 时,
时,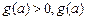 递增,
递增,
 在
在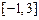 上的最小值为
上的最小值为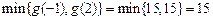
(Ⅲ) 如果
如果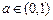 ,
,
则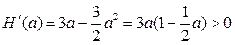
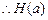 在
在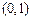 为递增函数,
为递增函数,
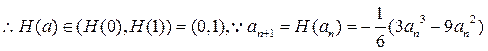
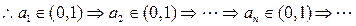
又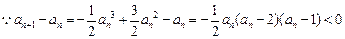
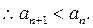

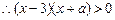 对
对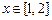 恒成立,
恒成立,又
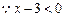 恒成立,
恒成立,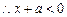 对
对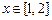 恒成立,
恒成立,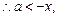 又
又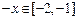 ,
,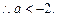 …
…(Ⅱ)由
 得:
得: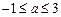 ,不妨设
,不妨设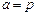 ,则q,r恰为方程两根,由韦达定理得:①
,则q,r恰为方程两根,由韦达定理得:①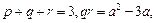
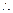 ②
②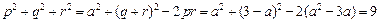
③而
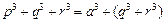
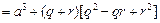

设
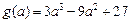 ,求导得:
,求导得: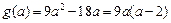
当
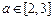 时,
时,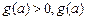 递增;当
递增;当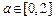 时,
时, 递减;
递减;当
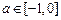 时,
时,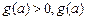 递增,
递增, 在
在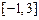 上的最小值为
上的最小值为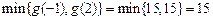
(Ⅲ)
 如果
如果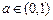 ,
,则
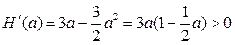
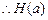 在
在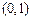 为递增函数,
为递增函数,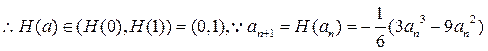
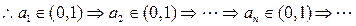
又
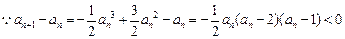
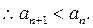

练习册系列答案
相关题目
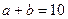 ,cosC是方程
,cosC是方程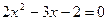 的一个根,求△ABC周长的最小值。
的一个根,求△ABC周长的最小值。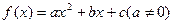 ,若存在
,若存在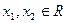 且
且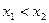 ,使得
,使得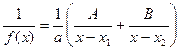 (其中A,B为常数),则称
(其中A,B为常数),则称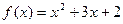 是否为“可分解函数”,若是,求出A,B的值;若不是,说明理由;
是否为“可分解函数”,若是,求出A,B的值;若不是,说明理由;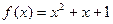 不是“可分解函数”;
不是“可分解函数”;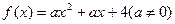 是“可分解函数”,则求a的取值范围,并写出A,B关于a的相应的表达式。
是“可分解函数”,则求a的取值范围,并写出A,B关于a的相应的表达式。
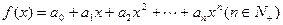 ,记
,记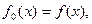
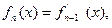 并且
并且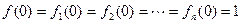 。
。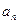 的表达式。
的表达式。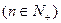
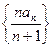 的前n项和为
的前n项和为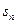
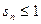
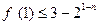
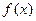 满足
满足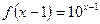 ,则函数
,则函数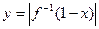 的图象是( )
的图象是( )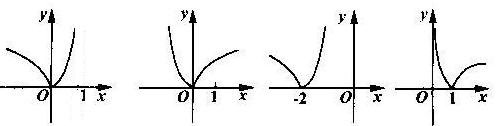
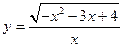 的定义域为
的定义域为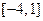
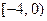
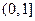
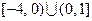
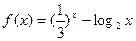 ,
,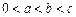 ,
,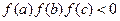 ,实数
,实数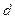 是函数
是函数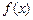 的一个零点.给出下列四个判断:
的一个零点.给出下列四个判断: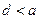 ;②
;②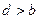 ;③
;③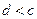 ;④
;④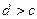 .
.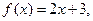 则函数
则函数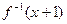 的反函数是
的反函数是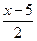
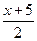
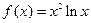 的单调递减区间为 .
的单调递减区间为 .