题目内容
(本小题满分13分)
设数列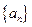 满足
满足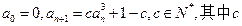 为实数
为实数
(Ⅰ)证明: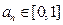 对任意
对任意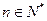 成立的充分必要条件是
成立的充分必要条件是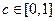 ;
;
(Ⅱ)设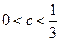 ,证明:
,证明: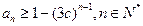 ;
;
(Ⅲ)设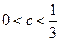 ,证明:
,证明: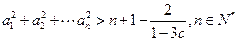
设数列
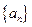 满足
满足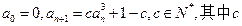 为实数
为实数(Ⅰ)证明:
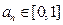 对任意
对任意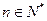 成立的充分必要条件是
成立的充分必要条件是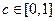 ;
;(Ⅱ)设
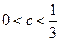 ,证明:
,证明: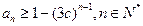 ;
;(Ⅲ)设
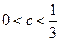 ,证明:
,证明: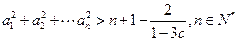
见解析
(1) 必要性:
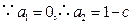 ,
,又
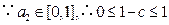 ,即
,即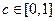
充分性:设
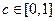 ,对
,对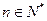 用数学归纳法证明
用数学归纳法证明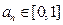
当
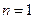 时,
时,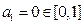 .假设
.假设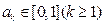
则
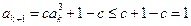 ,且
,且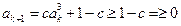
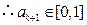 ,由数学归纳法知
,由数学归纳法知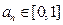 对所有
对所有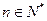 成立
成立(2) 设
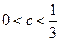 ,当
,当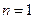 时,
时,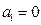 ,结论成立
,结论成立当
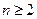 时,
时,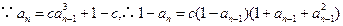
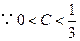 ,由(1)知
,由(1)知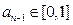 ,所以
,所以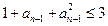 且
且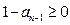
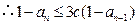
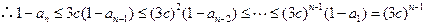
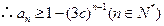
(3)设
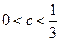 ,当
,当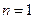 时,
时,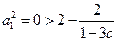 ,结论成立
,结论成立当
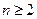 时,由(2)知
时,由(2)知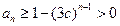
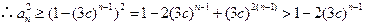

练习册系列答案
相关题目
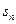 ,若
,若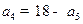 ,则
,则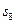 =
= 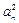 + 4n – 1 , nÎN*.
+ 4n – 1 , nÎN*.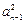 ="0" (n ³ 2);(2) 满足条件的数列不惟一,试至少求出数列{an}的的3个不同的通项公式 .
="0" (n ³ 2);(2) 满足条件的数列不惟一,试至少求出数列{an}的的3个不同的通项公式 .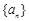 的公差
的公差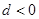 ,且
,且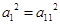 ,则数列
,则数列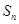 取最大值时
取最大值时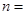 ( )
( )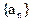 是等和数列且
是等和数列且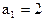 ,公和为5,那么
,公和为5,那么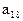 的值为_______,且这个数列前21项和
的值为_______,且这个数列前21项和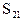 的值为_______。
的值为_______。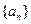 满足
满足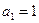 ,
, ,求
,求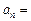 _______.
_______.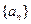 是等差数列,若
是等差数列,若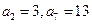 ,则数列
,则数列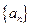 的前
的前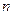 项和为
项和为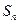 ,若
,若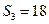 ,则
,则