题目内容
6.双曲线y=$\frac{1}{x}$在点(2,$\frac{1}{2}$)的切线方程是( )| A. | $\frac{1}{4}$x+y=0 | B. | $\frac{1}{4}$x-y=0 | C. | $\frac{1}{4}$x+y+1=0 | D. | $\frac{1}{4}$x+y-1=0 |
分析 先求曲线$\frac{1}{x}$的导数,因为函数在切点处的导数就是切线的斜率,求出斜率,再用点斜式写出切线方程,再化简即可.
解答 解:y=$\frac{1}{x}$的导数为y′=-$\frac{1}{{x}^{2}}$,
∴曲线y=$\frac{1}{x}$在点(2,$\frac{1}{2}$)处的切线斜率为-$\frac{1}{4}$
切线方程是y-$\frac{1}{2}$=-$\frac{1}{4}$(x-2),
化简得,$\frac{1}{4}$x+y-1=0
故选:D.
点评 本题主要考查了函数的导数与切线斜率的关系,属于导数的应用.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
16.双曲线C:$\frac{{x}^{2}}{5}$-$\frac{{y}^{2}}{3}$=1的左、右顶点分别为A1,A2,点P在C上且直线PA2斜率的取值范围是[-4,-2],那么直线PA1斜率的取值范围是( )
| A. | [-1,-$\frac{3}{10}$] | B. | [$\frac{3}{8}$,$\frac{3}{4}$] | C. | [-$\frac{3}{10}$,-$\frac{3}{20}$] | D. | [$\frac{3}{20}$,$\frac{3}{10}$] |
17.在△ABC中,三边a,b,c满足a2=b2+c2+bc,则角A等于( )
| A. | 30° | B. | 60° | C. | 120° | D. | 150° |
14.若坐标原点到抛物线x2=$\frac{1}{m}$y的准线距离为2,则m=( )
| A. | $\frac{1}{8}$ | B. | ±$\frac{1}{8}$ | C. | 8 | D. | ±8 |
1.关于函数f(x)=sinx+cosx,下列命题正确的是( )
| A. | f(x)最大值为2 | |
| B. | y=|f(x)|的最小正周期为2π | |
| C. | f(x)的图象关于点$(\frac{π}{4},0)$对称 | |
| D. | f(x)的图象向左平移$\frac{π}{4}$个单位后对应的函数是偶函数 |
18.函数f(x)=ex+x2+2x+1与g(x)的图象关于直线3x-y-2=0对称,P,Q分别是函数f(x),g(x)图象上的动点,则|PQ|的最小值为( )
| A. | $\frac{2\sqrt{10}}{5}$ | B. | $\frac{3\sqrt{10}}{10}$ | C. | $\frac{6\sqrt{10}}{10}$ | D. | $\frac{4\sqrt{10}}{5}$ |
15.设函数f(x)=(x+a)6,满足$\frac{f′(0)}{f(0)}$=-3,则f(x)的展开式中x4的系数为( )
| A. | -360 | B. | 360 | C. | -60 | D. | 60 |
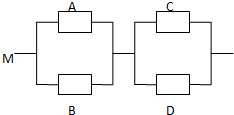 如图,用A、B、C、D表示四类不同的元件连接成系统M.当元件A、B至少有一个正常工作且元件C、D至少有一个正常工作时,系统M正常工作.已知元件A、B、C、D正常工作的概率依次为:0.3、0.6、0.5、0.8,元件连接成的系统M正常工作的概率P(M)=0.648.
如图,用A、B、C、D表示四类不同的元件连接成系统M.当元件A、B至少有一个正常工作且元件C、D至少有一个正常工作时,系统M正常工作.已知元件A、B、C、D正常工作的概率依次为:0.3、0.6、0.5、0.8,元件连接成的系统M正常工作的概率P(M)=0.648.