题目内容
16.已知空间三点A(0,2,3),B (-2,1,6),C(1,-1,5)(1)求以AB,AC为邻边的平行四边形面积
(2)求平面ABC一个法向量
(3)若向量$\overrightarrow a$分别与$\overrightarrow{AB}\;,\;\overrightarrow{AC}$垂直,且$|{\overrightarrow a}|=\sqrt{3}$求$\overrightarrow a$的坐标.
分析 (1)利用向量夹角公式可得:cosA,进而得到sinA,即可得出以AB,AC为邻边的平行四边形面积
S=$|\overrightarrow{AB}||\overrightarrow{AC}|$sinA.
(2)设平面ABC的一个法向量为$\overrightarrow n=(x\;,\;y\;,\;z)$,由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=0}\\{\overrightarrow{n}•\overrightarrow{AC}=0}\end{array}\right.$,解出即可得出.
(3)由于$\overrightarrow a⊥\overrightarrow{AB}$,$\overrightarrow a⊥\overrightarrow{AC}$,可得$\overrightarrow a$∥$\overrightarrow n$,设$\overrightarrow{a}$=λ$\overrightarrow{n}$,利用$|{\overrightarrow a}|=\sqrt{3}$,解得λ即可得出.
解答 解:(1)$\overrightarrow{AB}=(-2\;,\;-1\;,\;3)$,$\overrightarrow{AC}$=(1,-3,2),
$cos<\overrightarrow{AB},\overrightarrow{AC}>$=$\frac{\overrightarrow{AB}•\overrightarrow{AC}}{|\overrightarrow{AB}||\overrightarrow{AC}|}$=$\frac{7}{\sqrt{14}×\sqrt{14}}$=$\frac{1}{2}$,
S平行四边形ABCD=$|\overrightarrow{AB}||\overrightarrow{AC}|$$sin<\overrightarrow{AB},\overrightarrow{AC}>$
=$\sqrt{14}×\sqrt{14}$×$\frac{\sqrt{3}}{2}$=7$\sqrt{3}$.
(2)设平面ABC的一个法向量为$\overrightarrow n=(x\;,\;y\;,\;z)$,由$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AB}=0}\\{\overrightarrow{n}•\overrightarrow{AC}=0}\end{array}\right.$,可得$\left\{\begin{array}{l}{-2x-y+3z=0}\\{x-3y+2z=0}\end{array}\right.$,
取$\overrightarrow{n}$=(1,1,1).
(3)∵$\overrightarrow a⊥\overrightarrow{AB}$,$\overrightarrow a⊥\overrightarrow{AC}$,
∴$\overrightarrow a$∥$\overrightarrow n$,
设$\overrightarrow{a}$=λ(1,1,1),
∵$|{\overrightarrow a}|=\sqrt{3}$,解得λ=±1,
∴$\overrightarrow a$=±(1,1,1).
点评 本题考查了向量夹角公式、平行四边形面积、平面的法向量、向量垂直与数量积的关系、线面垂直的性质,考查了推理能力与计算能力,属于中档题.

| A. | $\frac{1}{4}$x+y=0 | B. | $\frac{1}{4}$x-y=0 | C. | $\frac{1}{4}$x+y+1=0 | D. | $\frac{1}{4}$x+y-1=0 |
| A. | $\frac{15}{2}$ | B. | $\frac{7}{2}$ | C. | 8 | D. | $\frac{17}{2}$ |
| A. | ① | B. | ② | C. | ③ | D. | 以上都不对 |
| A. | -1 | B. | 1 | C. | 0 | D. | ±1 |
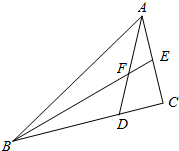 如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow{b}$,又$\overrightarrow{BD}$=2$\overrightarrow{DC}$,$|{\overrightarrow a}|=2,|{\overrightarrow b}|=1$,向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{3}$.
如图,在△ABC中,设$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AC}$=$\overrightarrow{b}$,又$\overrightarrow{BD}$=2$\overrightarrow{DC}$,$|{\overrightarrow a}|=2,|{\overrightarrow b}|=1$,向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{3}$.