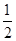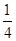题目内容
已知f(x)是定义在实数集R上的增函数,且f(1)=0,函数g(x)在(-∞,1]上为增函数,在[1,+∞)上为减函数,且g(4)=g(0)=0,则集合{x|f(x)g(x)≥0}等于( )
| A．{x|x≤0或1≤x≤4} |
| B．{x|0≤x≤4} |
| C．{x|x≤4} |
| D．{x|0≤x≤1或x≥4} |
A
画出函数f(x)和g(x)的草图如图所示,
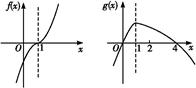
由图可知当f(x)g(x)≥0时,
x的取值范围是x≤0或1≤x≤4,
即{x|f(x)g(x)≥0}={x|x≤0或1≤x≤4}.故选A.
由图可知当f(x)g(x)≥0时,
x的取值范围是x≤0或1≤x≤4,
即{x|f(x)g(x)≥0}={x|x≤0或1≤x≤4}.故选A.
练习册系列答案
相关题目
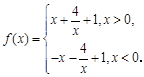
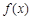的奇偶性；
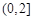和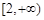
上的增减性；
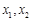满足：
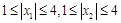，试证明：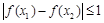
．
.
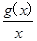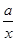，x∈(0，1]．
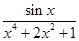的最大值与最小值的和为 .
)＜f(x)的x的取值范围是( )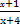
)的所有x之和为( )
=( )．
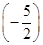