题目内容
设f(x)是连续的偶函数,且当x>0时是单调函数,则满足f(2x)=f(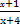 )的所有x之和为( )
)的所有x之和为( )
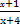 )的所有x之和为( )
)的所有x之和为( )A.- | B.- | C.-8 | D.8 |
C
∵f(x)是偶函数且x>0时,f(x)单调,
∴|2x|=|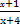 |,即2x(x+4)=±(x+1).
|,即2x(x+4)=±(x+1).
得2x2+9x+1=0或2x2+7x-1=0,
知共有四根.
∵x1+x2=- ,x3+x4=-
,x3+x4=- ,
,
∴所有x之和为- +(-
+(- )=-8.
)=-8.
∴|2x|=|
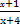 |,即2x(x+4)=±(x+1).
|,即2x(x+4)=±(x+1).得2x2+9x+1=0或2x2+7x-1=0,
知共有四根.
∵x1+x2=-
 ,x3+x4=-
,x3+x4=- ,
,∴所有x之和为-
 +(-
+(- )=-8.
)=-8.
练习册系列答案
相关题目
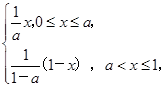 a为常数且a∈(0,1).
a为常数且a∈(0,1). 时,求f
时,求f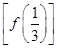 ;
; 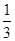 ,
,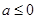 ”是“函数
”是“函数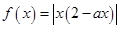 在区间
在区间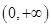 内单调递增”的( )
内单调递增”的( )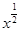 ,②y=
,②y=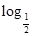 (x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数是____________.(填序号)
(x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数是____________.(填序号) ,若f(x)在(0,+∞)上单调递增,则实数a的取值范围为________.
,若f(x)在(0,+∞)上单调递增,则实数a的取值范围为________.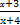 )的所有x之和为( )
)的所有x之和为( )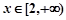 ,使不等式
,使不等式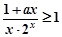 成立,则实数
成立,则实数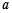 的最小值为 .
的最小值为 .