题目内容
已知函数g(x)=ax2-2ax+1+b(a≠0,b<1),在区间[2,3]上有最大值4,最小值1,设函数f(x)=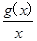 .
.
(1)求a、b的值及函数f(x)的解析式;
(2)若不等式f(2x)-k·2x≥0在x∈[-1,1]时有解,求实数k的取值范围.
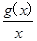 .
.(1)求a、b的值及函数f(x)的解析式;
(2)若不等式f(2x)-k·2x≥0在x∈[-1,1]时有解,求实数k的取值范围.
(1)a=1,b=0,g(x)=x2-2x+1,f(x)=x+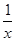 -2.(2)(-∞,1]
-2.(2)(-∞,1]
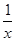 -2.(2)(-∞,1]
-2.(2)(-∞,1](1)g(x)=ax2-2ax+1+b,由题意得
①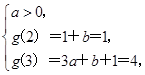 得
得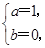
②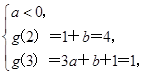 得
得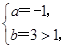 (舍).
(舍).
∴a=1,b=0,g(x)=x2-2x+1,f(x)=x+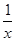 -2.
-2.
(2)不等式f(2x)-k·2x≥0,即2x+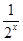 -2≥k·2x,
-2≥k·2x,
∴k≤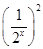 -2·
-2·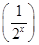 +1.
+1.
设t=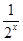 ,则k≤t2-2t+1,∵x∈[-1,1],故t∈
,则k≤t2-2t+1,∵x∈[-1,1],故t∈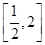 .
.
记h(t)=t2-2t+1,∵t∈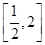 ,∴h(t)max=1,
,∴h(t)max=1,
故所求k的取值范围是(-∞,1]
①
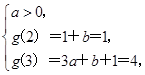 得
得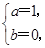
②
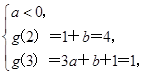 得
得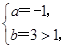 (舍).
(舍).∴a=1,b=0,g(x)=x2-2x+1,f(x)=x+
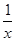 -2.
-2.(2)不等式f(2x)-k·2x≥0,即2x+
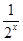 -2≥k·2x,
-2≥k·2x,∴k≤
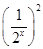 -2·
-2·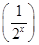 +1.
+1.设t=
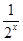 ,则k≤t2-2t+1,∵x∈[-1,1],故t∈
,则k≤t2-2t+1,∵x∈[-1,1],故t∈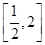 .
.记h(t)=t2-2t+1,∵t∈
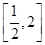 ,∴h(t)max=1,
,∴h(t)max=1,故所求k的取值范围是(-∞,1]

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
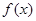 定义在(―1,1)上,对于任意的
定义在(―1,1)上,对于任意的 ,有
,有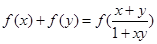 ,且当
,且当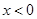 时,
时,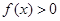 。
。 是否满足这些条件;
是否满足这些条件;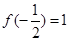 ,求方程
,求方程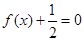 的解。
的解。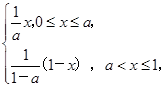 a为常数且a∈(0,1).
a为常数且a∈(0,1). 时,求f
时,求f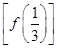 ;
; 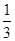 ,
,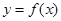 是定义域为
是定义域为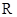 的偶函数. 当
的偶函数. 当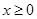 时,
时,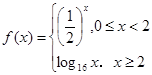 若关于
若关于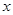 的方程
的方程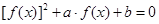
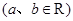 有且只有7个不同实数根,则实数
有且只有7个不同实数根,则实数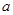 的取值范围是 .
的取值范围是 .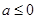 ”是“函数
”是“函数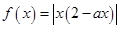 在区间
在区间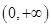 内单调递增”的( )
内单调递增”的( )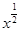 ,②y=
,②y=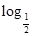 (x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数是____________.(填序号)
(x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数是____________.(填序号)