题目内容
已知函数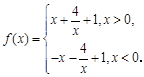
(1)判断函数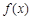 的奇偶性;
的奇偶性;
(2)试用函数单调性定义说明函数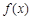 在区间
在区间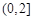 和
和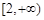 上的增减性;
上的增减性;
(3)若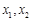 满足:
满足: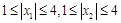 ,试证明:
,试证明: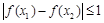 .
.
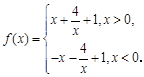
(1)判断函数
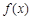 的奇偶性;
的奇偶性;(2)试用函数单调性定义说明函数
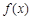 在区间
在区间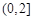 和
和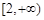 上的增减性;
上的增减性;(3)若
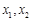 满足:
满足: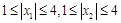 ,试证明:
,试证明: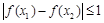 .
.(1)偶函数,(2)在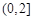 上是减函数,在
上是减函数,在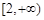 上是增函数(3)详见解析.
上是增函数(3)详见解析.
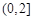 上是减函数,在
上是减函数,在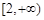 上是增函数(3)详见解析.
上是增函数(3)详见解析.试题分析:(1)判定函数奇偶性,首先判定函数定义域是否关于原点对称,然后再判断
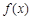 与
与 的相等或相反关系.本题定义域为一切实数,关于原点对称.函数
的相等或相反关系.本题定义域为一切实数,关于原点对称.函数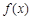 为分段函数,需分类讨论. 当
为分段函数,需分类讨论. 当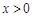 时,
时, ,
,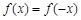 .当
.当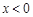 时,
时,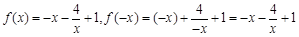 ,
,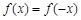 .故
.故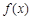 为偶函数.(2)利用定义研究函数单调性,需注重作差后的变形,关键是提取公因式,进行因式分解,以便判断符号.(3)由于
为偶函数.(2)利用定义研究函数单调性,需注重作差后的变形,关键是提取公因式,进行因式分解,以便判断符号.(3)由于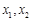 是同区间的两个任意数,所以只需证
是同区间的两个任意数,所以只需证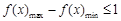 ,从而本题实质为求函数最值.由函数奇偶性及单调性知:
,从而本题实质为求函数最值.由函数奇偶性及单调性知: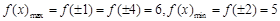 ,所以
,所以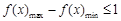 成立.
成立.试题解析:解:(1)∵当
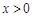 时,
时,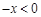 ,∴
,∴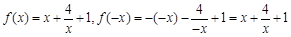
∴
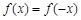 2分
2分∵当
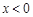 时,
时, ,∴
,∴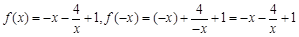
∴
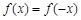 4分
4分∴对
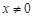 都有
都有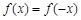 ,故
,故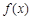 为偶函数 5分
为偶函数 5分(2)当
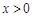 时,
时,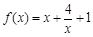
设
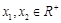 且
且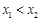 ,则
,则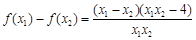 7分
7分∴当
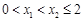 时,
时,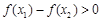 即
即
当
 时,
时,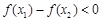 即
即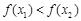 9分
9分∴函数
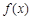 在区间
在区间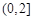 上是减函数,在区间
上是减函数,在区间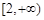 上是增函数 11分
上是增函数 11分(3)由(2)可知,当
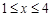 时:
时:若
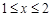 ,则
,则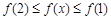 即
即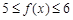
若
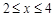 ,则
,则 即
即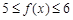
∴当
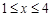 时,有
时,有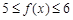 12分
12分又由(1)可知
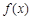 为偶函数,∴当
为偶函数,∴当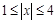 时,有
时,有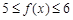 13分
13分∴若
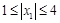 ,
,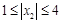 时,则
时,则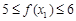 ,
, 14分
14分∴
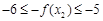 ,
,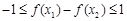 即
即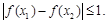 15分
15分
练习册系列答案
相关题目
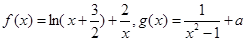
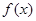 的单调区间.
的单调区间.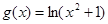 有4个不同的实根,求
有4个不同的实根,求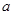 的范围?
的范围? ,使得关于
,使得关于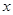 的方程
的方程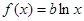 有两个不相等的实根?如果存在,求b
有两个不相等的实根?如果存在,求b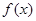 定义在(―1,1)上,对于任意的
定义在(―1,1)上,对于任意的 ,有
,有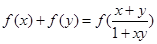 ,且当
,且当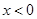 时,
时,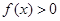 。
。 是否满足这些条件;
是否满足这些条件;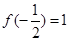 ,求方程
,求方程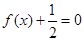 的解。
的解。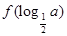 ≤2f(1),则a的取值范围是 ( )
≤2f(1),则a的取值范围是 ( )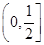
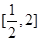
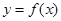 是定义域为
是定义域为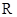 的偶函数. 当
的偶函数. 当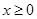 时,
时,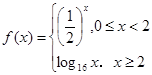 若关于
若关于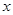 的方程
的方程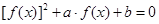
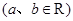 有且只有7个不同实数根,则实数
有且只有7个不同实数根,则实数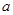 的取值范围是 .
的取值范围是 .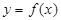 的定义域为
的定义域为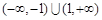 ,且其图象上任一点
,且其图象上任一点 满足方程
满足方程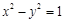 ,给出以下四个命题:
,给出以下四个命题: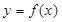 是偶函数;
是偶函数;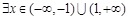 ,
,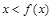 ;
;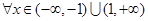 ,
,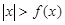 .其中真命题的个数是( )
.其中真命题的个数是( )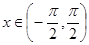 时,f(x)=x+sinx,则( )
时,f(x)=x+sinx,则( )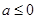 ”是“函数
”是“函数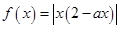 在区间
在区间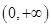 内单调递增”的( )
内单调递增”的( )