题目内容
已知椭圆C: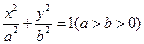 的长轴长为
的长轴长为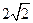 ,离心率
,离心率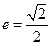 .
.
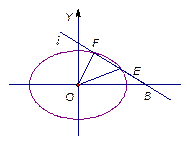
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若过点B(2,0)的直线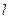 (斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且
(斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且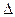 OBE与
OBE与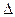 OBF的面积之比为
OBF的面积之比为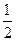 , 求直线
, 求直线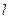 的方程.
的方程.
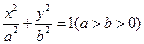 的长轴长为
的长轴长为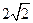 ,离心率
,离心率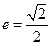 .
.
(Ⅰ)求椭圆C的标准方程;
(Ⅱ)若过点B(2,0)的直线
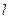 (斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且
(斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且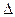 OBE与
OBE与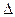 OBF的面积之比为
OBF的面积之比为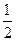 , 求直线
, 求直线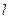 的方程.
的方程.解:(I)椭圆C的方程为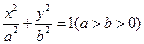 ,由题意知
,由题意知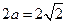 ,
,
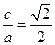 ,又
,又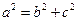 ,解得
,解得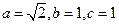
∴所求椭圆的方程为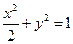 ………………4分
………………4分
(II)由题意知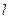 的斜率存在且不为零,
的斜率存在且不为零,
设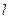 方程为
方程为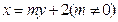 ①,将①代入
①,将①代入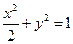 ,整理得
,整理得
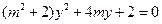 ,由
,由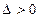 得
得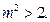 ………………6分
………………6分
设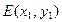 ,
,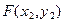 ,则
,则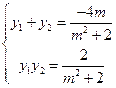 ② ………8分
② ………8分
由已知,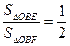 , 则
, 则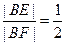
由此可知,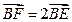 ,即
,即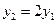 ………………………10分
………………………10分
代入②得,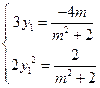 ,消去
,消去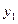 得
得
解得,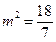 ,满足
,满足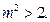 即
即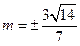 .
.
所以,所求直线 的方程为
的方程为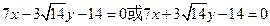 ……12分
……12分
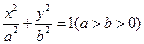 ,由题意知
,由题意知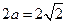 ,
, 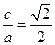 ,又
,又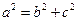 ,解得
,解得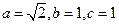
∴所求椭圆的方程为
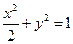 ………………4分
………………4分(II)由题意知
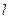 的斜率存在且不为零,
的斜率存在且不为零,设
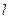 方程为
方程为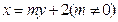 ①,将①代入
①,将①代入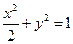 ,整理得
,整理得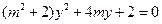 ,由
,由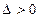 得
得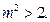 ………………6分
………………6分设
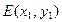 ,
,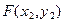 ,则
,则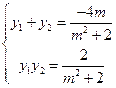 ② ………8分
② ………8分由已知,
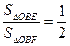 , 则
, 则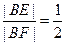
由此可知,
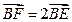 ,即
,即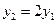 ………………………10分
………………………10分代入②得,
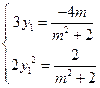 ,消去
,消去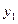 得
得
解得,
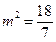 ,满足
,满足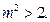 即
即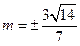 .
. 所以,所求直线
 的方程为
的方程为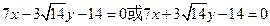 ……12分
……12分略

练习册系列答案
相关题目
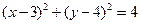
 取得最小值时点P的坐标.
取得最小值时点P的坐标. 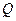 是
是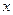 轴上的动点,
轴上的动点,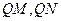 分别切圆
分别切圆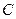 于
于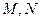 两点
两点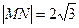 ,求直线
,求直线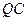 的方程;
的方程;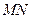 恒过一定点.
恒过一定点.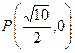 作倾斜角为
作倾斜角为 的直线与曲线
的直线与曲线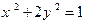 交于点
交于点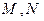 ,求
,求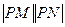 最小值及相应的
最小值及相应的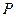 是抛物线
是抛物线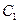 :
: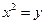 上动点。圆
上动点。圆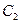 :
: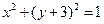 的圆心为点M,过点
的圆心为点M,过点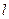 :
: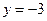 于
于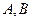 两点。(Ⅰ)求
两点。(Ⅰ)求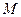 到抛物线
到抛物线 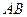 被抛物线
被抛物线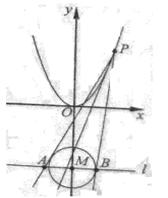
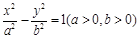 与直线
与直线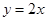 无交点,则离心率
无交点,则离心率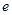 的取值范围是
的取值范围是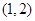
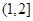
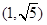
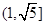
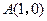 、
、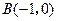 ,已知
,已知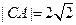 ,
,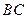 的垂直平分线
的垂直平分线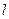 交
交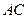 于
于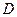 ,当点
,当点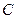 为动点时,点
为动点时,点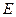 .
.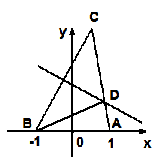
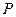 为
为 为坐标原点,曲线
为坐标原点,曲线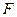 ,求
,求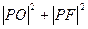 的最小值.
的最小值.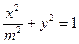 (常数
(常数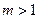 ),P是曲线C上的动点,M是曲线C的右
),P是曲线C上的动点,M是曲线C的右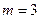 ,求|PA|的最大值与最小值.
,求|PA|的最大值与最小值.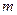 的取值范围.
的取值范围.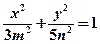 和双曲线
和双曲线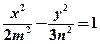 有公共的焦点,那么双曲线的离心率为 。
有公共的焦点,那么双曲线的离心率为 。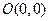 、
、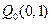 和
和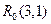 ,记
,记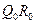 的中点为
的中点为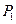 ,取
,取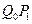 和
和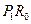 中的一条,记其端点为
中的一条,记其端点为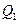 、
、 ,使之满足
,使之满足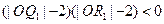 ;记
;记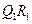 的中点为
的中点为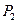 ,取
,取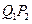 和
和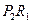 中的一条,记其端点为
中的一条,记其端点为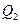 、
、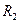 ,使之满足
,使之满足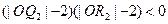 ;依次下去,得到点
;依次下去,得到点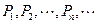 ,则
,则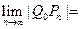 。
。