题目内容
(本题满分13分)已知圆C: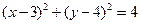
(1)若平面上有两点A(1 , 0),B(-1 , 0),点P是圆C上的动点,求使 取得最小值时点P的坐标.
取得最小值时点P的坐标.
(2) 若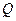 是
是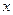 轴上的动点,
轴上的动点,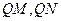 分别切圆
分别切圆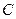 于
于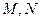 两点
两点
①若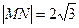 ,求直线
,求直线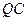 的方程;
的方程;
②求证:直线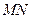 恒过一定点.
恒过一定点.
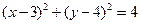
(1)若平面上有两点A(1 , 0),B(-1 , 0),点P是圆C上的动点,求使
 取得最小值时点P的坐标.
取得最小值时点P的坐标. (2) 若
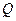 是
是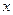 轴上的动点,
轴上的动点,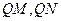 分别切圆
分别切圆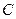 于
于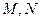 两点
两点①若
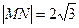 ,求直线
,求直线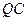 的方程;
的方程;②求证:直线
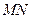 恒过一定点.
恒过一定点.解:(1)设P(x , y), 则由两点之间的距离公式知
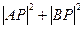 =
=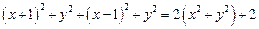 =2
=2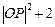
要使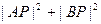 取得最小值只要使
取得最小值只要使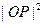 最小即可
最小即可
又P为圆上的点,所以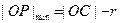 =
=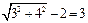 (
(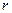 为
为 半径)
半径)
∴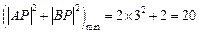 此时直线
此时直线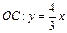
由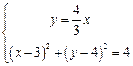 解得
解得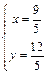 或
或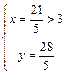 (舍去)
(舍去) ∴点P的坐标为
∴点P的坐标为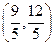
…………4分
(2)①设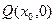 因为圆
因为圆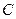 的半径
的半径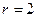 , 而
, 而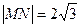 则
则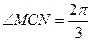 ,
,
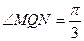 而
而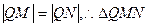 为等边三角形。
为等边三角形。
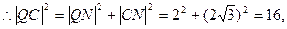 即
即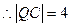
所求直线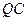 的方程:
的方程: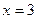 …………………8分
…………………8分
②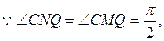 则
则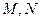 是以
是以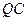 为直径的圆上。设
为直径的圆上。设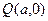 则
则
以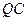 为直径的圆
为直径的圆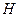 的方程:
的方程: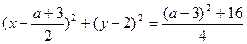 即
即
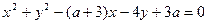 与圆
与圆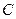 :
: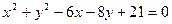 联立,消去
联立,消去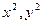 得
得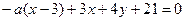 ,故无论取
,故无论取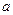 何值时,直线
何值时,直线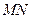 恒过一定点
恒过一定点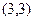 .13分
.13分
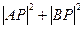 =
=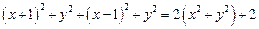 =2
=2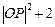
要使
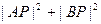 取得最小值只要使
取得最小值只要使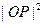 最小即可
最小即可又P为圆上的点,所以
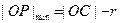 =
=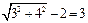 (
(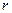 为
为 半径)
半径) ∴
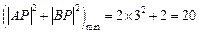 此时直线
此时直线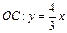
由
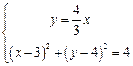 解得
解得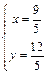 或
或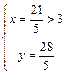 (舍去)
(舍去) ∴点P的坐标为
∴点P的坐标为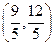
…………4分
(2)①设
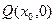 因为圆
因为圆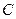 的半径
的半径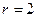 , 而
, 而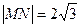 则
则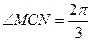 ,
,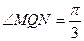 而
而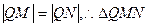 为等边三角形。
为等边三角形。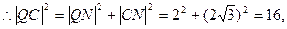 即
即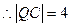
所求直线
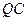 的方程:
的方程: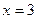 …………………8分
…………………8分②
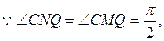 则
则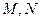 是以
是以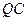 为直径的圆上。设
为直径的圆上。设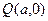 则
则以
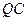 为直径的圆
为直径的圆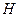 的方程:
的方程: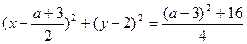 即
即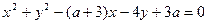 与圆
与圆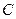 :
: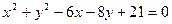 联立,消去
联立,消去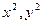 得
得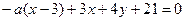 ,故无论取
,故无论取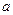 何值时,直线
何值时,直线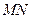 恒过一定点
恒过一定点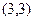 .13分
.13分略

练习册系列答案
相关题目
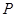 .为双曲线
.为双曲线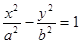 上的一点,
上的一点,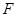 为一个焦点,以
为一个焦点,以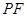 为直径的圆与圆
为直径的圆与圆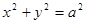 的位置关系是
的位置关系是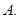 内切
内切 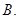 内切或外切
内切或外切 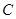 .外切
.外切 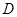 .相离或相交
.相离或相交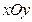 中,已知椭圆
中,已知椭圆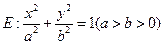 过点
过点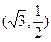 ,且椭圆
,且椭圆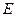 的离心率为
的离心率为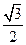
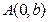 为直角顶点且内接于椭圆
为直角顶点且内接于椭圆 若存在,求出共有几个;若不存在,请说明理由
若存在,求出共有几个;若不存在,请说明理由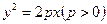 的焦点,斜率为
的焦点,斜率为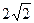 的直线交抛物线于
的直线交抛物线于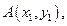
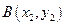 (
(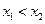 )两点,且
)两点,且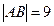
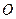 为坐标原点,
为坐标原点,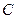 为抛物线上一点,若
为抛物线上一点,若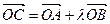 ,求
,求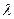 的值
的值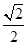 的直线
的直线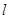 与椭圆
与椭圆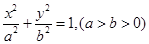 交于不同的两点,且这两个交点在
交于不同的两点,且这两个交点在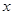 轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为( )
轴上的射影恰好是椭圆的两个焦点,则该椭圆的离心率为( )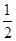
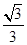

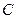 的右焦点为
的右焦点为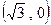 ,离心率为
,离心率为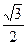
 :
: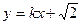 与椭圆
与椭圆 、
、 ,且
,且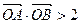 (其中
(其中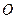 为原点),求实数
为原点),求实数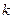 的取值范围
的取值范围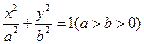 的左、右焦点分别为F1、F2.F2也是抛物线C2:
的左、右焦点分别为F1、F2.F2也是抛物线C2: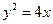 的焦点,点M为C1与C2在第一象限的交点,且
的焦点,点M为C1与C2在第一象限的交点,且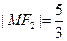 .
.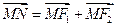 ,直线l∥MN,且与C1交于A、B两点,若
,直线l∥MN,且与C1交于A、B两点,若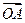 ·
·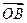 =0,求直线l的方程.
=0,求直线l的方程.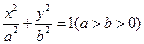 的长轴长为
的长轴长为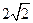 ,离心率
,离心率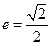 .
.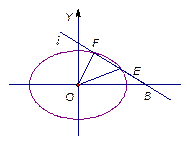
 (斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且
(斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且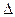 OBE与
OBE与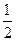 , 求直线
, 求直线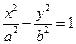 的渐近线为
的渐近线为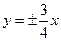 ,则双曲线的离心率为___________.
,则双曲线的离心率为___________.