题目内容
已知点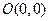 、
、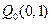 和
和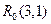 ,记
,记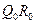 的中点为
的中点为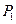 ,取
,取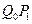 和
和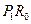 中的一条,记其端点为
中的一条,记其端点为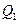 、
、 ,使之满足
,使之满足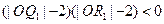 ;记
;记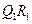 的中点为
的中点为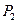 ,取
,取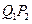 和
和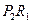 中的一条,记其端点为
中的一条,记其端点为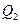 、
、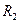 ,使之满足
,使之满足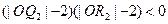 ;依次下去,得到点
;依次下去,得到点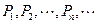 ,则
,则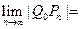 。
。
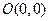 、
、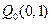 和
和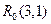 ,记
,记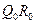 的中点为
的中点为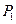 ,取
,取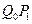 和
和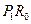 中的一条,记其端点为
中的一条,记其端点为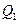 、
、 ,使之满足
,使之满足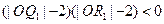 ;记
;记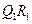 的中点为
的中点为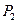 ,取
,取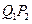 和
和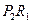 中的一条,记其端点为
中的一条,记其端点为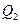 、
、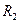 ,使之满足
,使之满足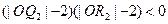 ;依次下去,得到点
;依次下去,得到点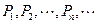 ,则
,则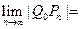 。
。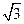
略

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案
相关题目
题目内容
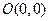 、
、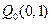 和
和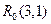 ,记
,记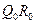 的中点为
的中点为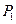 ,取
,取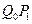 和
和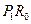 中的一条,记其端点为
中的一条,记其端点为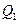 、
、 ,使之满足
,使之满足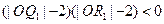 ;记
;记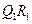 的中点为
的中点为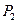 ,取
,取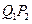 和
和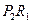 中的一条,记其端点为
中的一条,记其端点为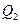 、
、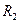 ,使之满足
,使之满足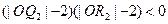 ;依次下去,得到点
;依次下去,得到点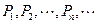 ,则
,则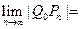 。
。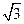

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案