题目内容
(本题满分15分)如图,设 是抛物线
是抛物线 :
: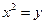 上动点。圆
上动点。圆 :
: 的圆心为点M,过点
的圆心为点M,过点 做圆
做圆 的两条切线,交直线
的两条切线,交直线 :
: 于
于 两点。(Ⅰ)求
两点。(Ⅰ)求 的圆心
的圆心 到抛物线
到抛物线  准线的距离。
准线的距离。
(Ⅱ)是否存在点 ,使线段
,使线段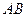 被抛物线
被抛物线 在点
在点 处得切线平分,若存在,求出点
处得切线平分,若存在,求出点 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
 是抛物线
是抛物线 :
: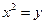 上动点。圆
上动点。圆 :
: 的圆心为点M,过点
的圆心为点M,过点 做圆
做圆 的两条切线,交直线
的两条切线,交直线 :
: 于
于 两点。(Ⅰ)求
两点。(Ⅰ)求 的圆心
的圆心 到抛物线
到抛物线  准线的距离。
准线的距离。(Ⅱ)是否存在点
 ,使线段
,使线段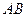 被抛物线
被抛物线 在点
在点 处得切线平分,若存在,求出点
处得切线平分,若存在,求出点 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
略
(Ⅰ)由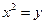 得准
得准 线方程为
线方程为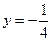 ,由
,由 得
得 又
又 即
即
同理 ,所以
,所以 是方程
是方程
 的两个不相等的根,从而
的两个不相等的根,从而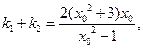
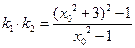 因为
因为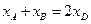 所以
所以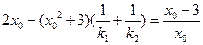 即
即
从而 进而得
进而得
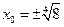 ,棕上所述,存在点
,棕上所述,存在点 满足题意,
满足题意,
点 的坐标为
的坐标为
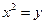 得准
得准 线方程为
线方程为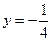 ,由
,由 得
得 又
又 即
即
同理
 ,所以
,所以 是方程
是方程 的两个不相等的根,从而
的两个不相等的根,从而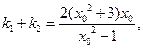
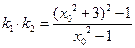 因为
因为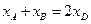 所以
所以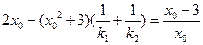 即
即
从而
 进而得
进而得
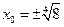 ,棕上所述,存在点
,棕上所述,存在点 满足题意,
满足题意,点
 的坐标为
的坐标为

练习册系列答案
相关题目
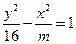 的离心率e=2,则m=____.
的离心率e=2,则m=____.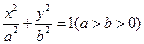 的长轴长为
的长轴长为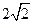 ,离心率
,离心率 .
.
 (斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且
(斜率不等于零)与椭圆C交于不同的两点E,F(E在B,F之间),且 OBE与
OBE与 , 求直线
, 求直线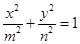 (
(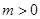 ,
, )的右焦点与抛物线
)的右焦点与抛物线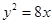 的焦点相同,离心率为
的焦点相同,离心率为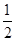 ,则此椭圆的方程为 ( )
,则此椭圆的方程为 ( )



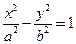 的渐近线为
的渐近线为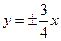 ,则双曲线的离心率为___________.
,则双曲线的离心率为___________.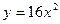 的焦点坐标为 。
的焦点坐标为 。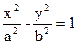 (a>0,b>0)上,C的焦距为4,则它的离心率为______
(a>0,b>0)上,C的焦距为4,则它的离心率为______ _______.
_______.
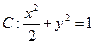 的右焦点为
的右焦点为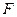 ,右准线为
,右准线为 ,点
,点 ,线段
,线段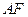 交
交 于点
于点
 ,若
,若 ,则
,则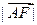 =" " .
=" " .