题目内容
某中学为丰富教工生活,国庆节举办教工趣味投篮比赛,有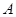 、
、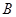 两个定点投篮位置,在
两个定点投篮位置,在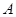 点投中一球得2分,在
点投中一球得2分,在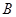 点投中一球得3分.其规则是:按先
点投中一球得3分.其规则是:按先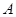 后
后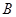 再
再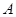 的顺序投
的顺序投
篮.教师甲在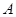 和
和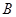 点投中的概率分别是
点投中的概率分别是 ,且在
,且在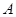 、
、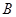 两点投中与否相互独立.
两点投中与否相互独立.
(1)若教师甲投篮三次,试求他投篮得分X的分布列和数学期望;
(2)若教师乙与甲在A、B点投中的概率相同,两人按规则各投三次,求甲胜乙的概率.
(1)分布列详见解析,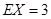 ;(2)
;(2)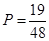 .
.
解析试题分析:本题主要考查独立事件、随机事件的分布列和数学期望等基础知识,考查学生的分析问题解决问题的能力和计算能力.第一问,先分析出教师甲投篮得分的不同情况,利用独立事件的概率的计算公式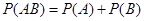 计算每一种情况的概率,列出分布列,利用
计算每一种情况的概率,列出分布列,利用 求出数学期望;第二问,先分析出甲胜乙的情况,包括甲得2分,3分,4分,5分,7分的情况,利用第一问的分布列的表格,第一种情况:甲得2分,乙得0分;第二种情况:甲得3分,乙得0分或2分;第三种情况::甲得4分,乙得0分或2分或3分;第四种情况:甲得5分,乙得0分或2分或3分或4分;第五种情况:甲得7分,乙得0分或2分或3分或4分或5分,求出每一种情况的概率再相见得到所求结论.
求出数学期望;第二问,先分析出甲胜乙的情况,包括甲得2分,3分,4分,5分,7分的情况,利用第一问的分布列的表格,第一种情况:甲得2分,乙得0分;第二种情况:甲得3分,乙得0分或2分;第三种情况::甲得4分,乙得0分或2分或3分;第四种情况:甲得5分,乙得0分或2分或3分或4分;第五种情况:甲得7分,乙得0分或2分或3分或4分或5分,求出每一种情况的概率再相见得到所求结论.
试题解析:设“教师甲在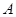 点投中”的事件为
点投中”的事件为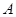 ,“教师甲在
,“教师甲在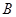 点投中”的事件为
点投中”的事件为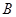 .
.
(1)根据题意知X的可能取值为0,2,3,4,5,7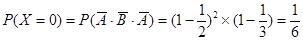 ,
,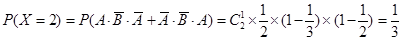
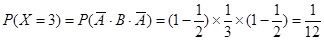
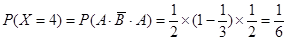
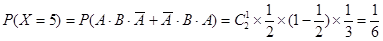
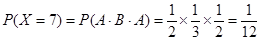 6分
6分
所以X的分布列是:X 0 2 3 4 5 7 P 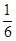
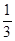
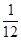
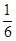
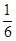
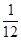
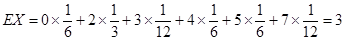 8分
8分
(2)教师甲胜乙包括:甲得2分、3分、4分、5分、7分五种情形.
这五种情形之间彼此互斥,因此,所求事件的概率 为:
为: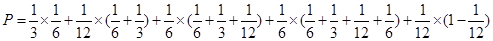
 12分
12分
考点:独立事件、随机事件的分布列和数学期望.

生产A,B两种元件,其质量按测试指标划分为:指标大于或等于82为正品,小于82为次品,现随机抽取这两种元件各100件进行检测,检测结果统计如下:
| 测试指标 | 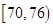 | 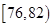 | 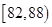 | 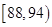 | 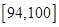 |
| 元件A | 8 | 12 | 40 | 32] | 8 |
| 元件B | 7 | 18 | 40 | 29 | 6 |
(2)生产一件元件A,若是正品可盈利50元,若是次品则亏损10元;生产一件元件B,若是正品可盈利100元,若是次品则亏损20元,在(1)的前提下;
(i)求生产5件元件B所获得的利润不少于300元的概率;
(ii)记X为生产1件元件A和1件元件B所得的总利润,求随机变量X的分布列和数学期望.
2014年2月21日,《中共中央关于全面深化改革若干重大问题的决定》明确:坚持计划生育的基本国策,启动实施一方是独生子女的夫妇可生育两个孩子的政策.为了解某地区城镇居民和农村居民对“单独两孩”的看法,某媒体在该地区选择了3600人调查,就是否赞成“单独两孩”的问题,调查统计的结果如下表:
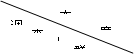 | 赞成 | 反对 | 无所谓 |
| 农村居民 | 2100人 | 120人 | y人 |
| 城镇居民 | 600人 | x人 | z人 |
(1)现在分层抽样的方法在所有参与调查的人中抽取360人进行问卷访谈,问应在持“无所谓”态度的人中抽取多少人?
(2)在持“反对”态度的人中,用分层抽样的方法抽取6人,按每组3人分成两组进行深入交流,求第一组中农村居民人数
 的分布列和数学期望.
的分布列和数学期望. 某产品的三个质量指标分别为x,y,z,用综合指标S=x+y+z评价该产品的等级.若S≤4,则该产品为一等品.先从一批该产品中,随机抽取10件产品作为样本,其质量指标列表如下:
| 产品编号 | A1 | A2 | A3 | A4 | A5 |
| 质量指标(x,y,z) | (1,1,2) | (2,1,1) | (2,2,2) | (1,1,1) | (1,2,1) |
| 产品编号 | A6 | A7 | A8 | A9 | A10 |
| 质量指标(x,y,z) | (1,2,2) | (2,1,1) | (2,2,1) | (1,1,1) | (2,1,2) |
(2)在该样品的一等品中,随机抽取两件产品,
①用产品编号列出所有可能的结果;
②设事件B为“在取出的2件产品中,每件产品的综合指标S都等于4”,求事件B发生的概率.

 和中位数
和中位数 (精确到整数分钟);
(精确到整数分钟);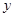 在上午
在上午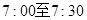 之间,而送报人每天在
之间,而送报人每天在 )的概率.
)的概率. .
.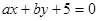 与圆
与圆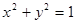 相切的概率;
相切的概率; 的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.
的值分别作为三条线段的长,求这三条线段能围成等腰三角形的概率.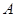 、
、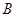 两个盒子中分别装有标记为
两个盒子中分别装有标记为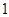 ,
,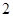 ,
, ,
,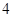 的大小相同的四个小球,甲从
的大小相同的四个小球,甲从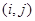 表示事件“甲抽到标号为
表示事件“甲抽到标号为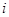 的小球,乙抽到标号为
的小球,乙抽到标号为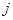 的小球”,试写出所有可能的事件;
的小球”,试写出所有可能的事件;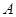 、
、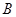 、
、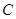 三道工序加工而成的,
三道工序加工而成的,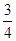 、
、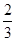 、
、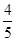 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场.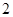 袋食品,求这2袋食品都为废品的概率;
袋食品,求这2袋食品都为废品的概率;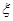 为加工工序中产品合格的次数,求
为加工工序中产品合格的次数,求