题目内容
小明家订了一份报纸,寒假期间他收集了每天报纸送达时间的数据,并绘制成频率分布直方图,如图所示.
(1)根据图中的数据信息,求出众数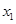 和中位数
和中位数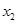 (精确到整数分钟);
(精确到整数分钟);
(2)小明的父亲上班离家的时间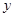 在上午
在上午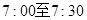 之间,而送报人每天在
之间,而送报人每天在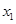 时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件
时刻前后半小时内把报纸送达(每个时间点送达的可能性相等),求小明的父亲在上班离家前能收到报纸(称为事件 )的概率.
)的概率.
(1)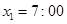 ,
,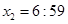 ;(2)
;(2)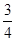
解析试题分析:(1)在频率分步直方图中,最高矩形的中点横坐标代表数据的众数;各个矩形的面积和为1,中位数是面积等分为 的轴线和横轴的交点;平均数是各矩形的面积乘以相应矩形中点横坐标的累加值;(2)基本事件总数有无限多个,故可以考虑几何概型.
的轴线和横轴的交点;平均数是各矩形的面积乘以相应矩形中点横坐标的累加值;(2)基本事件总数有无限多个,故可以考虑几何概型.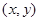 可以看成平面中的点,试验的全部结果构成平面区域
可以看成平面中的点,试验的全部结果构成平面区域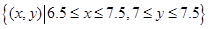 ,而事件A发生的前提是
,而事件A发生的前提是 ,利用面积的比表示事件A发生的概率
,利用面积的比表示事件A发生的概率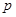 .
.
试题解析:(1)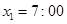 2分
2分
由频率分布直方图可知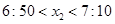 即
即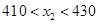 , 3分
, 3分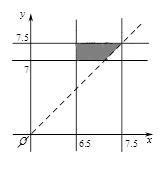
∴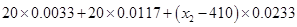
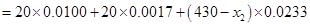
解得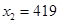 分即
分即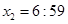 6分
6分
(2)设报纸送达时间为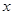 7分
7分
则小明父亲上班前能取到报纸等价于 , 10分
, 10分
如图可知,所求概率为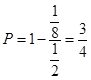 13分
13分
考点:1、频率分布直方图;2、众数和中位数;3、几何概型.

练习册系列答案
相关题目
下表是某市从3月份中随机抽取的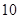 天空气质量指数(
天空气质量指数(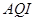 )和“
)和“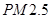 ”(直径小于等于
”(直径小于等于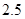 微米的颗粒物)
微米的颗粒物)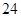 小时平均浓度的数据,空气质量指数(
小时平均浓度的数据,空气质量指数(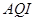 )小于
)小于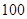 表示空气质量优良.
表示空气质量优良.
| 日期编号 | 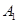 | 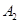 | 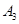 | 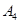 | 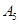 | 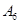 | 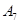 | 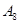 | 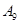 |  |
空气质量指数(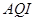 ) ) | 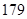 | 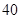 | 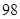 | 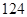 | 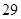 | 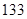 | 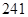 | 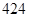 | 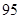 | 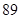 |
“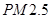 ” ”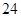 小时平均浓度( 小时平均浓度(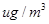 ) ) | 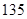 | 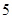 | 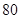 | 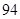 | 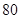 | 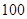 | 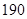 | 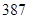 | 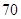 |  |
(1)根据上表数据,估计该市当月某日空气质量优良的概率;
(2)在上表数据中,在表示空气质量优良的日期中,随机抽取两个对其当天的数据作进一步的分析,设事件
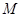 为“抽取的两个日期中,当天‘
为“抽取的两个日期中,当天‘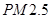 ’的
’的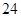 小时平均浓度不超过
小时平均浓度不超过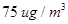 ”,求事件
”,求事件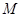 发生的概率.
发生的概率. 某商店试销某种商品20天,获得如下数据:
| 日销售量(件) | 0 | 1 | 2 | 3 |
| 频数 | 1 | 5 | 9 | 5 |
试销结束后(假设该商品的日销售量的分布规律不变),设某天开始营业时有该商品3件,当天营业结束后检查存货,若发现存货少于2件,则当天进货补充至3件,否则不进货,将频率视为概率。
(1)求当天商品不进货的概率;
(2)记X为第二天开始营业时该商品的件数,求X的分布列和数学期望。
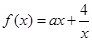 .
.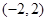 内任取一个实数
内任取一个实数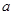 ,设事件
,设事件 ={函数
={函数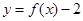 在区间
在区间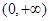 上有两个不同的零点},求事件
上有两个不同的零点},求事件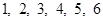 )得到的点数分别为
)得到的点数分别为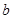 ,记事件
,记事件 {
{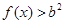 在
在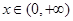 恒成立},求事件
恒成立},求事件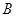 发生的概率.
发生的概率.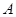 、
、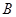 两个定点投篮位置,在
两个定点投篮位置,在 ,且在
,且在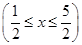 .
.