题目内容
某种食品是经过 、
、 、
、 三道工序加工而成的,
三道工序加工而成的, 、
、 、
、 工序的产品合格率分别为
工序的产品合格率分别为 、
、 、
、 .已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场.
.已知每道工序的加工都相互独立,三道工序加工的产品都为合格时产品为一等品;有两道合格为二等品;其它的为废品,不进入市场.
(1)正式生产前先试生产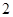 袋食品,求这2袋食品都为废品的概率;
袋食品,求这2袋食品都为废品的概率;
(2)设 为加工工序中产品合格的次数,求
为加工工序中产品合格的次数,求 的分布列和数学期望.
的分布列和数学期望.
(1)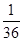 ;(2)分布列见详见,
;(2)分布列见详见,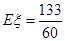 .
.
解析试题分析:(1) 求出2袋食品的三道工序都不合格的概率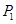 ,②有一袋食品三道工序都不合格,另一袋有两道工序不合格的概率
,②有一袋食品三道工序都不合格,另一袋有两道工序不合格的概率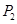 ,③两袋都有两道工序不合格的概率
,③两袋都有两道工序不合格的概率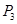 ,则所求的概率为
,则所求的概率为 ;(2)由题意可得
;(2)由题意可得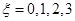 ,求出离散型随机变量的取每个值的概率,即得
,求出离散型随机变量的取每个值的概率,即得 的分布列,由分布列求出期望.
的分布列,由分布列求出期望.
试题解析:(1)2袋食品都为废品的情况为
①2袋食品的三道工序都不合格 .
.
②有一袋食品三道工序都不合格,另一袋有两道工序不合格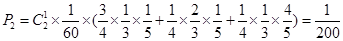 .
.
③两袋都有两道工序不合格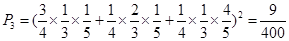 ,
,
所以2袋食品都为废品的概率为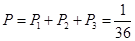 .
.
(2)
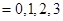
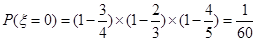
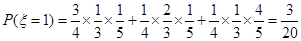 ,
,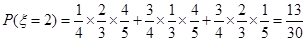 ,
,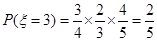 .
.


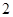
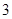

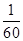
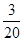
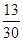
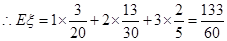 .
.
考点:1、相互独立事件的概率乘法公式;2、离散型随机变量及其分布列;3、离散型随机变量的期望与方差.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
气象部门提供了某地区今年六月份(30天)的日最高气温的统计表如下:
| 日最高气温t(单位:℃) | t≤22 | 22<t≤28 | 28<t≤32 | t>32 |
| 天数 | 6 | 12 | Y | Z |
某水果商根据多年的销售经验,六月份的日最高气温t(单位:℃)对西瓜的销售影响如下表:
| 日最高气温t(单位:℃) | t≤22 | 22<t≤28 | 28<t≤32 | t>32 |
| 日销售额X(单位:千元) | 2 | 5 | 6 | 8 |
(2)若视频率为概率,求六月份西瓜日销售额的期望和方差;
(3)在日最高气温不高于32℃时,求日销售额不低于5千元的概率.
 、
、 两个定点投篮位置,在
两个定点投篮位置,在 ,且在
,且在 .
. ,求
,求
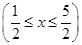 .
.