Question

【题目】已知函数 ，其中a为实数．
（1）当 时，求曲线y=f（x）在点（1，f（1））处的切线方程；
（2）当x≥ 时，若关于x的不等式f（x）≥0恒成立，试求a的取值范围．

Answer 1

【答案】
（1）解：当a=﹣ 时， ，f（1）=e﹣1，

， ．

故曲线y=f（x）在点（1，f（1））处的切线方程为：y﹣e+1= （x﹣1），

即

（2）解：由f（x）≥0，得 ，

∵ ，∴ ．

令 ，则 = ．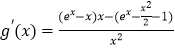

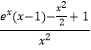令h（x）= ，则h′（x）=x（ex﹣1）．

∵x ，∴h′（x）＞0，即h（x）在[ ）上单调递增．

∴h（x）≥h（ ）= ．

∴g′（x）＞0．故g（x）在[ ）上单调递增．

则g（x）≥ ．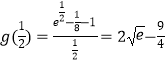

∴a的取值范围是

【解析】（1）把a=﹣ 代入函数解析式，求出f（1），求出函数的导函数，得到f′（1），由点斜式写出切线方程；（2）把不等式f（x）≥0恒成立转化为 恒成立．利用导数求函数 的最小值，则a小于等于函数g（x）的最小值，答案可求．