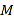题目内容
【题目】(选修4﹣5:不等式选讲)
已知函数f(x)=|2x﹣1|+|2x+a|,g(x)=x+3.
(1)当a=﹣2时,求不等式f(x)<g(x)的解集;
(2)设a>﹣1,且当 ![]() 时,f(x)≤g(x),求a的取值范围.
时,f(x)≤g(x),求a的取值范围.
【答案】
(1)解:当a=﹣2时,求不等式f(x)<g(x)化为|2x﹣1|+|2x﹣2|﹣x﹣3<0.
设y=|2x﹣1|+|2x﹣2|﹣x﹣3,则 y= 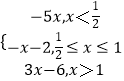 ,它的图象如图所示:
,它的图象如图所示:
结合图象可得,y<0的解集为(0,2),故原不等式的解集为(0,2).
(2)解:设a>﹣1,且当 ![]() 时,f(x)=1+a,不等式化为 1+a≤x+3,故 x≥a﹣2对
时,f(x)=1+a,不等式化为 1+a≤x+3,故 x≥a﹣2对 ![]() 都成立.
都成立.
故﹣ ![]() ≥a﹣2,解得 a≤
≥a﹣2,解得 a≤ ![]() ,故a的取值范围为(﹣1,
,故a的取值范围为(﹣1, ![]() ].
].
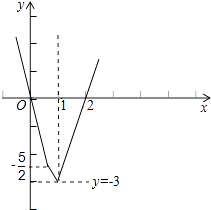
【解析】(1)当a=﹣2时,求不等式f(x)<g(x)化为|2x﹣1|+|2x﹣2|﹣x﹣3<0.设y=|2x﹣1|+|2x﹣2|﹣x﹣3,画出函数y的图象,数形结合可得结论.(2)不等式化即 1+a≤x+3,故 x≥a﹣2对 ![]() 都成立.故﹣
都成立.故﹣ ![]() ≥a﹣2,由此解得a的取值范围.
≥a﹣2,由此解得a的取值范围.
【考点精析】本题主要考查了函数单调性的性质和绝对值不等式的解法的相关知识点,需要掌握函数的单调区间只能是其定义域的子区间 ,不能把单调性相同的区间和在一起写成其并集;含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号才能正确解答此题.

【题目】自2017年2月底,90多所自主招生试点高校将陆续出台2017年自主招生简章,某校高三年级选取了在期中考试中成绩优异的100名学生作为调查对象,对是否准备参加2017年的自主招生考试进行了问卷调查,其中“准备参加”“不准备参加”和“待定”的人数如表:
准备参加 | 不准备参加 | 待定 | |
男生 | 30 | 6 | 15 |
女生 | 15 | 9 | 25 |
(1)在所有参加调查的同学中,在三种类型中用分层抽样的方法抽取20人进行座谈交流,则在“准备参加”“不准备参加”和“待定”的同学中应各抽取多少人?
(2)在“准备参加”的同学中用分层抽样方法抽取6人,从这6人中任意抽取2人,求至少有一名女生的概率.