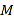��Ŀ����
����Ŀ����ͼ������P��ABCD�У�PA��ƽ��ABCD���ı���ABCD��ֱ�����Σ�����DA��AB��AD��BC��PA=2AD=BC=2��AB=2 ![]() ��
�� 
��1��������ֱ��PC��AD���ɽǵĴ�С��
��2����ƽ��ABCD����һ������C������E���������ϵ���һ����Q������PQ��AD���ɽǵĴ�Сǡ����PC��AD���ɽǣ����ж�����E����״��˵�����ɣ�
��3����ƽ��ABCD�ڣ����Q�ǣ�2�����е�����E��ֱ������ABCD�ڲ��������߽磩��һ������CG�ϵĶ��㣬����GΪ����E��DC�Ľ��㣮��BΪԲ�ģ�BQΪ�뾶r��Բ�ֱ������εı�AB��BC����M��N���㣮��Q�������߶�CG���˶�ʱ������Բ�뾶r�ķ�Χ��VP��BMN�ķ�Χ��
���𰸡�
��1���⣺��ͼ����AΪԭ�㣬ֱ��ABΪx�ᡢֱ��ADΪy�ᡢֱ��APΪz�ᣬ�����ռ�ֱ������ϵ��
������P��0��0��2���� ![]() ��D��0��1��0����
��D��0��1��0����
���� ![]() ����
���� ![]() ��
��
������ֱ��PC��AD���ɽǦ����� 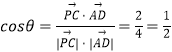 ��
��
��������ֱ��PC��AD���ɽǵĴ�СΪ ![]()
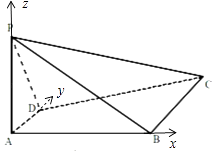
��2���⣺���Q��x��y��0������P��0��0��2������D��0��1��0������A��0��0��0����
�� ![]() ��
�� ![]() ��
��
�� ![]() ��
�� ![]() ��
��
���������õ�3y2��x2=4��
������E��ƽ��ABCD�ڵ�˫����
��3���⣺����ͼ��ʾ��xOy������ϵ�У���ΪD��0��1���� ![]() ��
�� ![]() ����G��x1��y1��������
����G��x1��y1�������� ![]() ����DC�ķ���Ϊ
����DC�ķ���Ϊ ![]() ��
��
����˫����E��3y2��x2=4�ķ��̿ɵã�3y2��8��y��1��2=45y2��16y+12=0������ ![]() ��
��
��Ϊֱ��DC��˫����E���ڵ�C���� ![]() �������ɵ�
�������ɵ� ![]() ����
���� ![]() ��
��
��˫����E��ֱ������ABCD�ڲ��������߽磩���������� ![]() ��
�� ![]() ��
��
����Q��x��y��Ϊ˫����CG�ϵĶ��㣬 ![]() ��
��
���ԣ� ![]()
��Ϊ ![]() �����Ե�
�����Ե� ![]() ʱ��
ʱ�� ![]() ��
��
�� ![]() ʱ��
ʱ�� ![]() ��
��
��ҪʹԲB��AB��BC���н��㣬��|BQ|��2��
�����������Բ�İ뾶ȡֵ��Χ�� ![]() ��
��
��ΪPA��DMN������P��DMN���Ϊ ![]() �����������ת��Ϊ�о���BMN�����������Ϊ��MBNΪֱ�ǣ����ԡ�BMN��Ϊ����ֱ�������Σ�
�����������ת��Ϊ�о���BMN�����������Ϊ��MBNΪֱ�ǣ����ԡ�BMN��Ϊ����ֱ�������Σ�
��ǰ������ ![]() ����|BM|=|BN|=r��
����|BM|=|BN|=r��
������� ![]() ������
������ ![]() ��
��
���ǣ� ![]() ��
��
����Q���˶������C�غ�ʱ�����ȡ�����ֵ����Q���˶��������� ![]() ʱ��
ʱ��
��|BQ|������Сʱ�����ȡ����Сֵ����

����������1����ͼ����AΪԭ�㣬ֱ��ABΪx�ᡢֱ��ADΪy�ᡢֱ��APΪz�ᣬ�����ռ�ֱ������ϵ�����������нǹ�ʽ���ɵó�����2�����Q��x��y��0������P��0��0��2������D��0��1��0������A��0��0��0�������� ![]() �������������ɵó�����3����G��x1 �� y1������
�������������ɵó�����3����G��x1 �� y1������ ![]() ����DC�ķ���Ϊ����˫����E��3y2��x2=4�ķ��̿ɵã��ɵ�y1y2 �� �ɵ�G����˫����E��ֱ������ABCD�ڲ��������߽磩����������
����DC�ķ���Ϊ����˫����E��3y2��x2=4�ķ��̿ɵã��ɵ�y1y2 �� �ɵ�G����˫����E��ֱ������ABCD�ڲ��������߽磩���������� ![]() ��
�� ![]() ��������Q��x��y��Ϊ˫����CG�ϵĶ��㣬��������֮����빫ʽ���䷶Χ���ɵó���
��������Q��x��y��Ϊ˫����CG�ϵĶ��㣬��������֮����빫ʽ���䷶Χ���ɵó���
�����㾫����������Ŀ����֪��������������ֱ�������ɵĽǺͿռ���������������������֪ʶ���Եõ�����Ĵ𰸣���Ҫ��������ֱ�����ɽǵ���1��ƽ�Ʒ���������ֱ���е�һ��ֱ����ѡ��һ����㣬����һ����ƽ���ߣ�2�����η����ѿռ�ͼ�β�����Ϥ�Ļ������ļ����壬�������塢ƽ�������塢������ȣ���Ŀ��������������������ֱ��Ĺ�ϵ��![]() ����
����![]() �ij���
�ij���![]() ��
��![]() ��
��![]() �ķ����ϵ�ͶӰ
�ķ����ϵ�ͶӰ![]() �ij˻���
�ij˻���

 ��ս�п�����ϵ�д�
��ս�п�����ϵ�д�