Question

【题目】在平面直角坐标系xOy中,设圆x2+y2-4x=0的圆心为Q.

(1)求过点P(0,-4)且与圆Q相切的直线的方程;

(2)若过点p(0,-4)且斜率为k的直线与圆Q相交于不同的两点A,B,以OA、OB为邻边做平行四边形OABC,问是否存在常数k,使得平行四边形OABC为矩形?请说明理由.

Answer 1

【答案】（1）=.（2）存在常数,使平行四边形OABC得为矩形.

【解析】试题分析：（1）考虑直线斜率是否存在，当斜率存在时，设切线方程为: ，根据圆心到直线的距离等于半径求出，即可求得直线的方程；（2）联立得，写出根与系数的关系，根据矩形的性质，利用向量可求出的值.

试题解析：(1)由题意知,圆心Q坐标为(2,0)，半径为2

当直线斜率不存在时，直线方程为，符合题意

当直线斜率存在时，设切线方程为:

∴由,解得

∴所求的切线方程为=.

(2)假设存在满足条件的实数,则设,

联立得,

∵

∴ (或由(1)知),

∴且= =,

∵==

∴==,

又∵==,

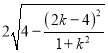∴要使平行四边形OABC为矩形，则==

∴

∴存在常数，使平行四边形OABC得为矩形.