题目内容
2.函数f(x)=sinx+x3.数列{an}的前n项和为Sn=pn2+qn,p,q为常数,且an∈(-$\frac{π}{2}$,$\frac{π}{2}$),若f(a10)<0,则f(a1)+f(a2)+…+f(a18)+f(a19)取值( )| A. | 恒为正数 | B. | 恒为负数 | C. | 恒为零 | D. | 可正可负 |
分析 运用奇偶性的定义,判断f(x)为奇函数,再由导数判断f(x)递增,判断数列为等差数列,由等差数列的性质和函数的单调性和奇偶性,结合倒序求和,即可判断所求取值符号.
解答 解:由f(x)=sinx+x3.可得
f(-x)=sin(-x)+(-x)3=-(sinx+x3)=-f(x),
则f(x)为奇函数,且f(0)=0,
由f(x)的导数为cosx+3x2>0在(-$\frac{π}{2}$,$\frac{π}{2}$)恒成立,
即有f(x)在(-$\frac{π}{2}$,$\frac{π}{2}$)递增,
数列{an}的前n项和为Sn=pn2+qn,则an=Sn-Sn-1=pn2+qn-p(n-1)2-q(n-1)=2pn+q-p,
n=1时,a1=S1=q+p,则数列{an}为等差数列,
即有a1+a19=a2+a18=…=2a10,
由f(a10)<0=f(0),可得a10<0,
则a1<-a19,a2<-a18,…,a11<-a9,
即有f(a1)<f(-a19)=-f(a19)
即为f(a1)+f(a19)<0,
同理可得f(a2)+f(a18)<0,
…,f(a11)+f(a9)<0,
设S=f(a1)+f(a2)+…+f(a18)+f(a19),
S=f(a19)+f(a18)+…+f(a2)+f(a1),
则2S=[f(a1)+f(a19)]+[f(a2)+f(a18)]+…+[f(a19)+f(a1)]<0,
即有S<0.
故选B.
点评 本题考查函数的性质和运用,主要考查函数的奇偶性和单调性的应用,考查等差数列的通项和求和公式,同时考查倒序求和的方法,考查推理能力,属于中档题.

练习册系列答案
 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
10.已知复数z=i2013+(i+1)5,则z的虚部是( )
| A. | 4 | B. | 3 | C. | -4 | D. | -3 |
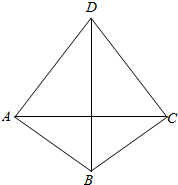 如图,在四边形ABCD中,AC=$\sqrt{3}$,∠ABC=120°,∠BAD=∠BCD=90°,则BD的长为4.
如图,在四边形ABCD中,AC=$\sqrt{3}$,∠ABC=120°,∠BAD=∠BCD=90°,则BD的长为4.