题目内容
14.如图所示的三个游戏盘中(图(1)是正方形,图(2)是半径之比为1:2的两个同心圆,图(3)是正六边形)各有一个玻璃小球,一次摇动三个游戏盘后,将它们水平放置,就完成了一局游戏.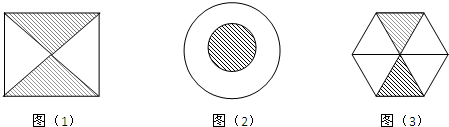
(1)一局游戏后,这三个盘中的小球都停在阴影部分的概率是多少?
(2)用随机变量ξ表示一局游戏后小球停在阴影部分的个数与小球没有停在阴影部分的个数之差的绝对值,求随机变量ξ的分布列及数学期望.
分析 (1)一局游戏后,分别求出三个盘中停在阴影部分的概率,由此利用互相独立事件同时发生的概率计算公式能求出一局游戏后,这三个盘中的小球都停在阴影部分的概率.
(2)一局游戏后,小球停在阴影部分的次数可能取值为0,1,2,3,相应的小球没有停在阴影部分的次数可能取值为3、2、1、0,从而得到ξ可能取值为1、3,分别求出相应的概率,由此能求出随机变量ξ的分布列及数学期望.
解答 解:(1)一局游戏后,三个盘中停在阴影部分分别记为事件A1,A2,A3,
由题意知A1,A2,A3互相独立,且${P(A}_{1})=\frac{1}{2}$,P(A2)=$\frac{1}{4}$,P(A3)=$\frac{1}{3}$,
∴一局游戏后,这三个盘中的小球都停在阴影部分的概率为:
P(A1A2A3)=P(A1)P(A2)P(A3)=$\frac{1}{2}×\frac{1}{4}×\frac{1}{3}$=$\frac{1}{24}$.
(2)一局游戏后,小球停在阴影部分的次数可能取值为0,1,2,3,
相应的小球没有停在阴影部分的次数可能取值为3、2、1、0,
∴ξ可能取值为1、3,
则P(ξ=3)=P(A1A2A3)+P($\overline{{A}_{1}}\overline{{A}_{2}}\overline{{A}_{3}}$)
=P(A1)P(A2)P(A3)+$P(\overline{{{A}_{1}}^{\;}})P(\overline{{A}_{2}})P(\overline{{A}_{3}})$
=$\frac{1}{2}×\frac{1}{4}×\frac{1}{3}+\frac{1}{2}×\frac{3}{4}×\frac{2}{3}$=$\frac{7}{24}$,
P(ξ=1)=1-$\frac{7}{24}=\frac{17}{24}$,
所以ξ分布列为:
| ξ | 1 | 3 |
| P | $\frac{17}{24}$ | $\frac{7}{24}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意互相独立事件同时发生的概率计算公式的合理运用.

| A. | 恒为正数 | B. | 恒为负数 | C. | 恒为零 | D. | 可正可负 |
| A. | P<R<Q | B. | R<Q<P | C. | R<P<Q | D. | Q<R<P |
| A. | $\frac{\sqrt{2}}{6}$ | B. | $\frac{\sqrt{3}}{6}$ | C. | $\frac{\sqrt{2}}{4}$ | D. | $\frac{\sqrt{3}}{4}$ |
| 工作代码 | 紧前工作 | 紧后工作 | 工期/时 |
| A | C | G | 2 |
| B | D | 无 | 3 |
| C | 无 | A、D、F | 4 |
| D | C | B | 2 |
| E | F | 无 | 4 |
| F | C | E | 2 |
| G | A | 无 | 5 |
 如图,过点P作⊙O的切线PA,A为切点,过PA中点B作割线交⊙O于C、D,连结PC并延长⊙O于E,连结PD,交⊙O于F,求证:EF∥PA.
如图,过点P作⊙O的切线PA,A为切点,过PA中点B作割线交⊙O于C、D,连结PC并延长⊙O于E,连结PD,交⊙O于F,求证:EF∥PA. 如图所示,一个铸铁零件,是由半个圆柱与一个正四棱柱组合成的几何体,圆柱的底面直与高均为2厘米,正四棱柱底面边长为2厘米、侧棱为3厘米,求该零件的质量(铁的密度约为7.4克厘米3)(精确到0.1克).
如图所示,一个铸铁零件,是由半个圆柱与一个正四棱柱组合成的几何体,圆柱的底面直与高均为2厘米,正四棱柱底面边长为2厘米、侧棱为3厘米,求该零件的质量(铁的密度约为7.4克厘米3)(精确到0.1克).